Abstract
The present work is a topical review of the theoretical research on the quantum theory of plasmons and plasmon–photon interaction. The plasmons are defined as the quanta of the quantized plasmonic field. The corresponding classical plasmonic field was constructed on the basis of the study of collective oscillations of the electron gas in the solid. The electron–electron Coulomb interaction is taken into account. The explicit forms of the plasmon–photon interaction Lagrangian in canonical quantum mechanics and the plasmon–photon interaction action functional in the functional integral approach are derived. They all show that the interaction processes are nonlocal ones. The physical origin of the nonlocality is the complex structure of plasmons as composite quasiparticles: they cannot be considered as point particles, as was assumed in all phenomenological theories.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The resonance phenomenon in collective oscillations of electron gas was demonstrated by early works on plasma oscillations in solids [1–4]. It was caused by the elementary collective excitations behaving like quasiparticles of a special type called plasmons. In recent years there has been significant progress in the study of the interaction processes in which plasmons play the essential role, and a new very promising area of quantum physics called plasmonics has emerged and was rapidly developed. The variety of plasmonic processes and phenomena is quite broad: the formation of hybrid systems consisting of semiconductor quantum dots and metallic nanoparticles [5, 6], interaction between a metallic nanoparticle and a dipole emitter [7], exciton–plasmon coupling (plexciton) [8–10], exciton–plasmon resonance energy transfer [11, 12], plasmon-enhanced light absorption [13, 14] and fluorescence [15–20], plasmonic-molecular resonance [21–28]. The results of the research on plasmonic processes have led to the creation of plasmonic nanoantennae for various efficient applications [29].
In our previous works [30–32] attempts were made to elaborate the quantum theory of plasmon enabling one to exactly derive the effective action functional, or the effective Hamiltonians in the special cases, of the interactions of plasmons with other quasiparticles in the matter as well as with the electromagnetic field, starting from first principles of electrodynamics and quantum physics. The present article is a topical review of the above-mentioned theoretical works with the extension to include also the derivation of the effective action functional of the interacting photon–plasmon system.
In section 2, applying the canonical quantization procedure of quantum mechanics, we present the theory of canonical quantization of the plasmonic field [31]. The construction of the quantum plasmonic field by means of the functional integral technique is performed in section 3 [30, 32]. In section 4 the effective action functional of the interacting photon–plasmon system is derived by means of the canonical quantization method in quantum mechanics. The same subject as that of section 4 is studied in section 5 in the framework of the functional integral approach. The conclusion and discussions are presented in section 6.
2. Quantum plasmonic field in canonical quantum mechanics
Consider the system of itinerant electrons moving in the electrostatic field generated by the positive charge of the ions in some crystal. Denote n(x, t) the electron density (number of electrons per unit volume) and n0 its mean value averaged over both space and time. The average charge density –en0 of electrons, –e being the negative electron charge, compensates the average positive charge of ions in the crystal, and the fluctuating charge density in the crystal is determined by the expression

According to the Coulomb law, the charge distribution with the density (1) in a special region V generates a time-dependent electrical field with the potential
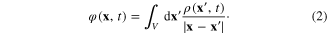
From formula (2) it follows the Poisson equation
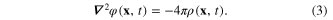
The mutual interaction between electrons of the electron gas in the region V gives rise to the potential energy of the electron gas
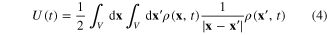
which can be also represented in the form

On the other side, as the consequence of the oscillating displacements of electrons, the fluctuation of the electron density n(r, t) generates the total kinetic energy of the electron gas. Denote 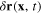 the displacement vector of the electron having the coordinate x at the time moment t, and m the electron mass. Since the electron has the velocity
the displacement vector of the electron having the coordinate x at the time moment t, and m the electron mass. Since the electron has the velocity
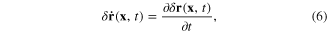
the whole electron gas has following total kinetic energy
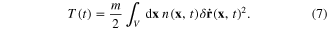
Consider now the conservation of the total electron number. Denote dNS the number of electrons going through the boundary S of a region V from the inside of V into its outside during the time interval from t to t + dt
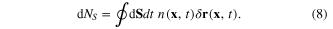
Using the Ostrogradski–Gauss formula, we rewrite dNS as follows
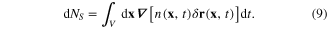
The decrease of the electron number inside V during that time interval equals
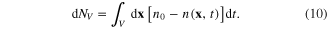
Because of the conservation of the total electron number, there must be the equality
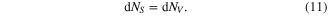
From equations (1) and (9)–(11) it follows that
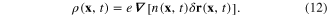
For the convenience in performing the canonical quantization procedure we decompose the functions 
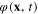 and
and  into the Fourier series, using a basis consisting of the plane waves satisfying the periodic boundary conditions at the opposite surfaces of a cube with the volume V and normalized in this cube. We have the following formulae
into the Fourier series, using a basis consisting of the plane waves satisfying the periodic boundary conditions at the opposite surfaces of a cube with the volume V and normalized in this cube. We have the following formulae
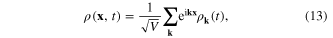

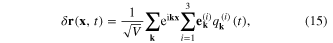
where  for each k are three unit vectors satisfying the conditions
for each k are three unit vectors satisfying the conditions
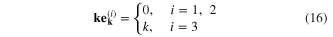
 Two terms with i = 1, 2 are the transverse displacements, while that with i = 3 is the longitudinal displacement along the direction of the wave vector k. From equation (3) and formulae (13) and (14) we obtain
Two terms with i = 1, 2 are the transverse displacements, while that with i = 3 is the longitudinal displacement along the direction of the wave vector k. From equation (3) and formulae (13) and (14) we obtain
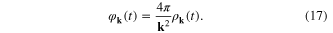
Consider the approximation in which the fluctuating electron density n(x, t) in the expression of ρ(x, t) is replaced by its average value n0
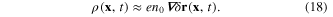
In this case from the expressions (13) and (15) and equation (18) we obtain
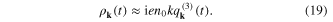
Therefore the potential energy (4) and the kinetic energy (7) are expressed in terms of the generalized coordinates of the system as follows
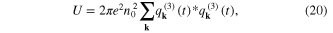

Lagrangian of the electron gas as a classical mechanical system has the expression
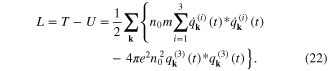
The equations of motion are
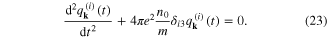
It follows that the transverse coordinates 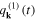 and
and 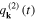 do not oscillate, while the longitudinal one
do not oscillate, while the longitudinal one 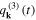 periodically oscillates with the angular frequency
periodically oscillates with the angular frequency
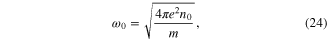
which is the know plasma frequency of a free electron gas. Since the transverse coordinates do not oscillate, we discard them and replace the notation  by the simpler one
by the simpler one 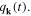 Lagrangian of the system becomes
Lagrangian of the system becomes
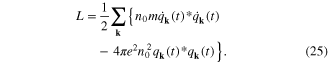
Now we demonstrate that the quantum mechanical system with the Lagrangian (25) can be considered as a classical field 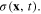 Consider the Fourier transformation of this classical field and its time derivative
Consider the Fourier transformation of this classical field and its time derivative

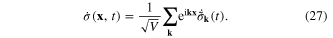
We have
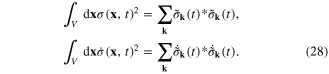
Setting
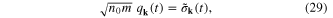
we can represent Lagrangian (25) as that of a real scalar field 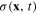
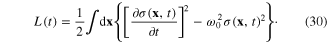
This expression is similar to the Lagrangian of a Klein–Gordon real scalar field in the relativistic field theory except for the absence of the term containing the spatial derivative  of the scalar field
of the scalar field 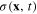 [33–36]. The action functional of this field is
[33–36]. The action functional of this field is
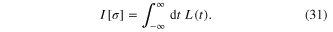
Now we apply the canonical quantization procedure to the real scalar field with the Lagrangian (30). Denote 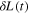 and
and 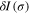 the variations of L(t) and I[σ] when the scalar field
the variations of L(t) and I[σ] when the scalar field  and is time derivative
and is time derivative 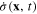 are subjected by the infinitely small variations
are subjected by the infinitely small variations 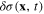 and
and  ,
,
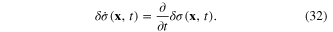
We have
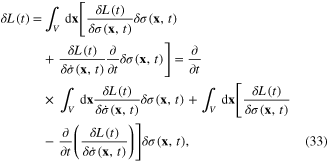
and therefore

Because of the boundary condition
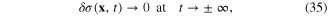
the first term in the right-hand side of equation (34) vanishes, and we obtain
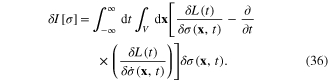
On the other hand, by definition
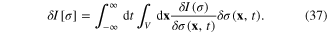
The comparison of formulae (36) and (37) gives
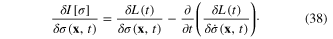
From the extreme action principle
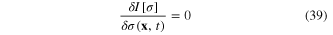
we obtain Lagrange functional equation
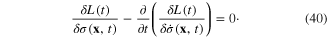
Considering  as the canonical coordinate of the field, we have following canonical momentum
as the canonical coordinate of the field, we have following canonical momentum
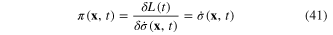
and Hamiltonian functional
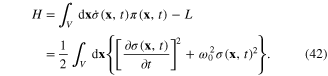
After the canonical quantization procedure, the canonical coordinate 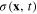 and momentum
and momentum  become the operators
become the operators 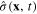 and
and  and we have following Hamiltonian operator of the quantized field
and we have following Hamiltonian operator of the quantized field
Now we expand the canonical field operator  into the Fourier series of the orthogonal and normalized plane waves
into the Fourier series of the orthogonal and normalized plane waves
Substituting expression (44) of  into the right hand side of formula (43), after lengthy standard calculations we obtain
into the right hand side of formula (43), after lengthy standard calculations we obtain
According to the equation (41), the canonical momentum 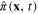 equals the time derivative of the canonical field
equals the time derivative of the canonical field  Therefore
Therefore  has following expansion
has following expansion
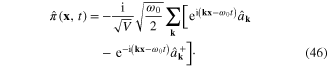
Inverting the expansions (44) and (46), we obtain the expressions of 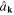 and
and 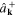 in terms of the canonical coordinate
in terms of the canonical coordinate 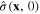 and momentum
and momentum  :
:
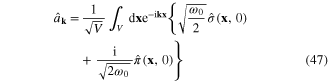
and
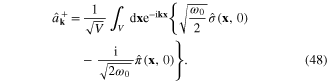
According to the canonical quantization rules, between the operators  and
and 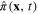 there exist the following equal-time canonical commutation relations
there exist the following equal-time canonical commutation relations
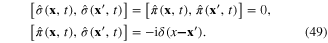
Using two expressions (47) and (48) and commutation relations (49), we derive the following canonical commutation relations
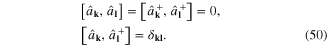
These relations together with formula (45) for Hamiltonian  show that
show that  and
and 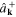 are the destruction and creation operators of the quasiparticles with the energy ω0—the plasmons. Thus, we have constructed the quantum field
are the destruction and creation operators of the quasiparticles with the energy ω0—the plasmons. Thus, we have constructed the quantum field  whose quanta are the plasmons—the quantum plasmonic field. In the harmonic approximation the plasmons are dispersionless. In order to establish the dispersion law of the plasmons by means of the canonical quantization procedure it is necessary to go beyond the harmonic approximation.
whose quanta are the plasmons—the quantum plasmonic field. In the harmonic approximation the plasmons are dispersionless. In order to establish the dispersion law of the plasmons by means of the canonical quantization procedure it is necessary to go beyond the harmonic approximation.
3. Quantum plasmonics field in functional integral formalism
3.1. Basic notions in functional integral method
Consider a physical structure in three-dimensional space, for any vector x in this space we introduce the vector
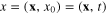
in the corresponding four-dimensional space–time and denote
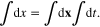
The integration domain in the three-dimensional space is the whole volume Ω of the structure, while the integral over t is calculated from 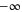 to
to 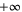 .
.
Let  be a real scalar function of x. Considering each value
be a real scalar function of x. Considering each value  as a component of a vector with the continuous vector index x, we extend the notion of multiple integral and introduce the notion of functional integral as follows
as a component of a vector with the continuous vector index x, we extend the notion of multiple integral and introduce the notion of functional integral as follows

Similarly, let 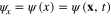 and
and  be two other hermitian conjugate spinor functions. Considering
be two other hermitian conjugate spinor functions. Considering 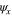 and
and 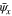 as the spinor components of two vectors with the continuous vector index x, we introduce the notion of functional integral over
as the spinor components of two vectors with the continuous vector index x, we introduce the notion of functional integral over 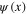 and
and 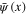 as the extension of the definition of the multiple integral to the case of two uncountable sets of integration variables
as the extension of the definition of the multiple integral to the case of two uncountable sets of integration variables  and
and 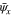 with the continuous index x
with the continuous index x

The functional integral method was a powerful method for the study of relativistic quantum field theory [33–36].
The subject of our study is the electron gas inside the volume Ω of a physical structure. Because the electrons are confined inside this volume, we impose on the functional integration variables the following boundary condition: they must vanish outside volume Ω as well as on its surface.
The Bosonic functional integration variables  are commuting
are commuting
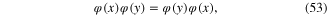
while the fermionic ones 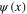 and
and 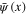 anticommute each other
anticommute each other

Functional integration variables 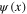 and
and 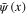 are called the Grassmann variables. Beside of these dynamical variables one often uses also Grassmann parameter
are called the Grassmann variables. Beside of these dynamical variables one often uses also Grassmann parameter 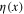 and its hermitian conjugate
and its hermitian conjugate 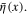 They anticommute each other
They anticommute each other
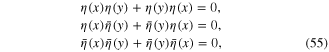
and also anticommute with the dynamical Grassmann variables
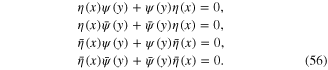
Bosonic functional integration variable commutes with all Grassmann dynamical variables and Grassmann parameters
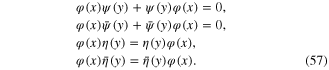
In the calculations we often use the functional derivation operators  and
and 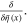 They anticommute each other
They anticommute each other
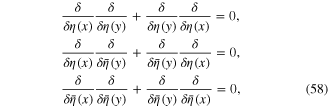
anticommute with fermionic integration variables
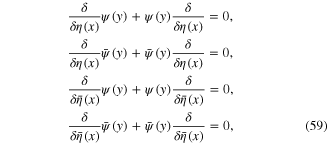
but commute with the Bosonic integration variable
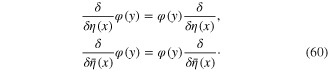
From the above-mentioned anticommutativity property of fermionic integration variables 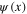 and
and  Grassmann parameters
Grassmann parameters 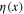 and
and 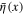 and functional derivation operators
and functional derivation operators 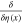 and
and 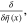 it is straightforward to derive the following formulae which are often used:
it is straightforward to derive the following formulae which are often used:
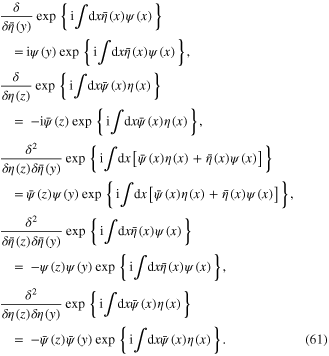
Denote 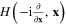 the Hamiltonian of the electron with mass m moving in a confining potential U(x)
the Hamiltonian of the electron with mass m moving in a confining potential U(x)
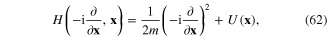
and
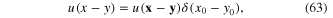
where u(x − y) is the potential energy of the Coulomb repulsion between two electrons
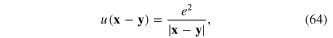
e is the electron charge. The key mathematical tools of the functional integral method in quantum plasmonics are the functional integrals
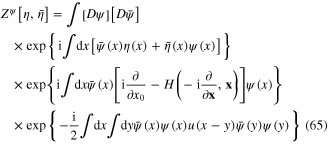
and
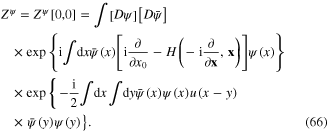
When the electron–electron Coulomb interaction is neglected, instead of the functional integrals (65) and (66) we have the following ones
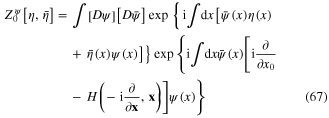
and
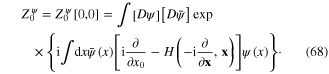
Expressions in formulae (65) and (67) are called the generating functionals.
The Grassmann dynamical variables 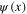 and
and  can be considered as a fermionic field and its hermitian conjugate. In the case of the electron gas with the electron–electron Coulomb repulsion, the action functional of the field
can be considered as a fermionic field and its hermitian conjugate. In the case of the electron gas with the electron–electron Coulomb repulsion, the action functional of the field 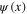 is
is
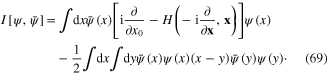
If the electron–electron Coulomb repulsion is neglected, the action functional of the system becomes
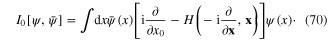
Thus, the functional integrals  and
and 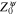 of the electron gas are expressed in terms of its action functional
of the electron gas are expressed in terms of its action functional ![$I\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn75.gif) and
and ![${{I}_{0}}\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn76.gif) as follows
as follows
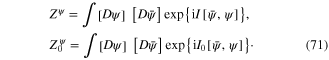
In general, for any physical system described by a set of the fields 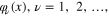 between the action functional
between the action functional ![$I\left[ {{\varphi }_{\nu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn78.gif) of this system and its functional integral
of this system and its functional integral 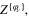 the relation of the form
the relation of the form
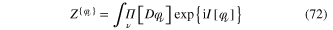
always holds.
3.2. Green functions
Now we define the Green functions and derive the relations between them. Since these relations represent the dynamics of the corresponding quantum field, the functional integral method can be considered as a new method of the field quantization.
Considering Grassmann dynamical variables 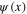 and
and  as a fermionic field and its hermitian conjugate, we define the average (also called expectation value) of any product
as a fermionic field and its hermitian conjugate, we define the average (also called expectation value) of any product  over all configurations of this field as follows:
over all configurations of this field as follows:
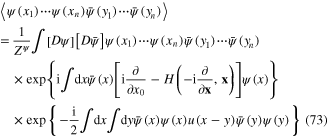
when the electron–electron Coulomb interaction is taken into account, and

when the electron–electron Coulomb interaction is neglected and electron field is called the free field.
Let us consider in detail the case of free electron field. The average of the product  over all field configurations is called two–point (one—particle) Green function
over all field configurations is called two–point (one—particle) Green function
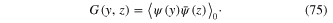
From the expression (67) of the generating functional ![$Z_{0}^{\psi }\left[ \eta ,\bar{\eta } \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn84.gif) it follows that
it follows that
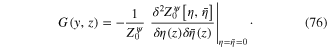
Similarly, the average of the product  over all field configurations is called four-point (two-particle) Green function
over all field configurations is called four-point (two-particle) Green function
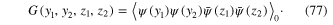
It is expressed in terms of ![$Z_{0}^{\psi }\left[ \eta ,\bar{\eta } \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn86.gif) as follows
as follows
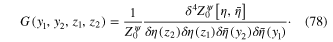
In order to establish the explicit form of the generating functional (67) we consider the Schrӧdinger equation
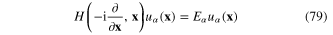
and introduce  the solution of the inhomogeneous differential equation
the solution of the inhomogeneous differential equation
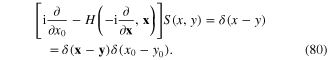
S(x, y) has the general form
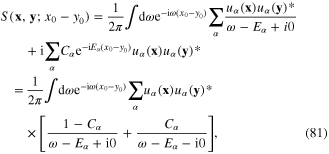
where the constants 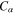 are related with the parameters of the electron gas. Their physical meanings will be clarified latter.
are related with the parameters of the electron gas. Their physical meanings will be clarified latter.
Now let us perform the shift of the functional integration variables
in the rhs of formula (68) for the constant 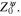 The functional integral in this formula must be invariant under the shift (82) of the functional integration variables. After lengthy but standard transformations and calculations we obtain the following formula
The functional integral in this formula must be invariant under the shift (82) of the functional integration variables. After lengthy but standard transformations and calculations we obtain the following formula

Comparing the rhs of relation (83) with the definition (67) of ![$Z_{0}^{\psi }\left[ \eta ,\bar{\eta } \right],$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn90.gif) we derive the explicit expression of this generating functional
we derive the explicit expression of this generating functional
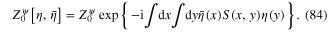
From expression (84) and formula (76) we obtain
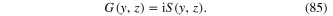
Similarly, from expression (84) and formula (78) we derive a relation between four-point and two-point Green functions
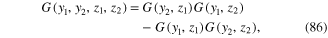
which is the well-known Wick theorem for the four-point Green function of the free electron field. By means of the same reasonnings as those above presented, we can verify the validity of the Wick theorem for any 2n point Green function of the free electron field.
Now we consider again formula (81) for the function  Note that the limit
Note that the limit  of the average of the product
of the average of the product 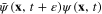 is the particle density
is the particle density 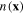 :
:
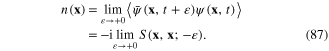
From formula (81) for 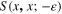 it follows that
it follows that
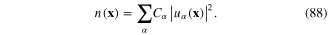
Thus, Cα is the electron occupation number nα at the quantum state with the wave function uα(x): Cα = nα.
3.3. Scalar field of collective oscillations in electron gas
Now we study the system of interacting electrons with the following functional integral
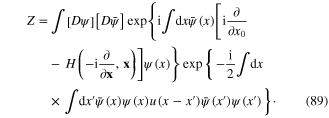
The Coulomb term in the functional integral (89) is bilinear with respect to the electron density 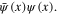 We linearize this bilinear interaction Hamiltonian by introducing a scalar field
We linearize this bilinear interaction Hamiltonian by introducing a scalar field  playing the role of the order parameter of collective oscillations in the electron gas and using the following functional integral
playing the role of the order parameter of collective oscillations in the electron gas and using the following functional integral

Performing a shift of the functional integration variable
we rewrite  in a new form
in a new form
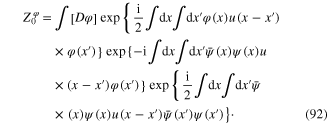
From this relation we derive the celebrated Hubbard–Stratonovich transformation
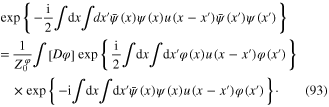
Substititing the expression in the rhs. of relation (93) instead of its lhs. which is a factor in the rhs. of formula (89), we transform the functional integral Z into the form

According to the definition (74) for the average of an expression over all field configurations, formula (94) can be rewritten as follows
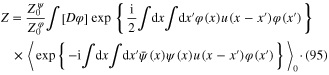
Expanding the exponential function

into a functional power series of the scalar field, we obtain
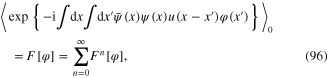

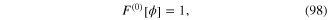
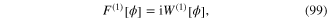
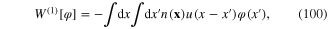
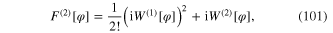
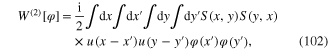

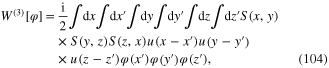
and so on. Continuing similar calculations in higher orders, finally we obtain
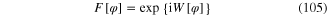
with
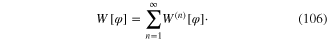
Using expression (95) and relations (96)–(106), we obtain the functional integral Z expressed in term of the scalar field  only
only
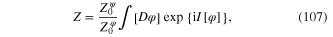
with the effective action functional
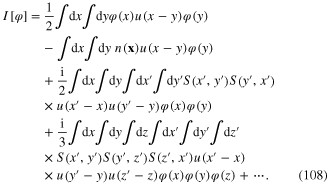
In the approximation of the second order with respect to the scalar field 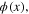 the effective action can be written as follows
the effective action can be written as follows
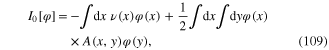
where
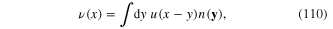
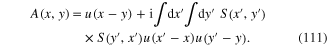
From the principle of extreme action
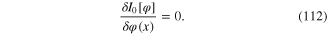
We derive the dynamical equation for the scalar field  corresponding to the extreme action
corresponding to the extreme action
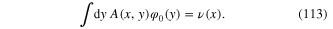
It has the solution
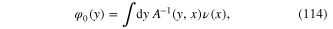
where 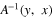 is the kernel of the integral operator inverse to that with the kernel
is the kernel of the integral operator inverse to that with the kernel 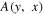 :
:
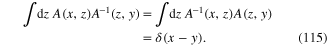
The extreme value of the action functional equals

The fluctuations of the scalar field 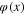 around the extreme field
around the extreme field 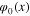 are described by the difference
are described by the difference
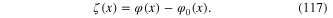
In terms of this new field  the effective action
the effective action ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn107.gif) has the quadratic form
has the quadratic form

The dynamical equation for the field 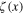 is
is

For testing the validity of above-presented functional integral formalism now we apply it to the simple case of a homogeneous electron gas in the three-dimensional space. In this case function S(x, y) depends only on the difference x–y of the coordinates and has the Fourier transformation
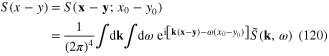
with the Fourier transform
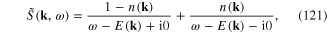
where E(k) is the kinetic energy E(k) = k2/2m of the electron with momentum k, n(k) is the electron occupation number at the state with momentum k, 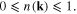 Function A(x, y) determined by formula (111) also depends only on the difference x–y and has following Fourier transformation
Function A(x, y) determined by formula (111) also depends only on the difference x–y and has following Fourier transformation
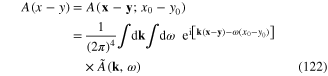
with the Fourier transform
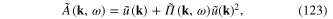
where
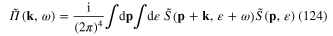
and 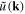 is the Fourier transform of
is the Fourier transform of 
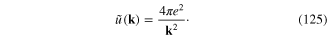
The dynamical equation (119) becomes
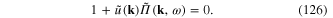
This equation determines the dependence of ω on k- the plasmon dispersion ω(k). In order to establish the dispersion we must calculate  After the integration of the rhs of formula (124) with respect to the variable
After the integration of the rhs of formula (124) with respect to the variable  , we obtain
, we obtain
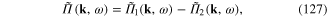
where
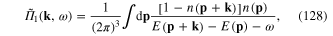
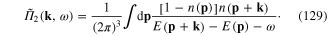
By means of the substitution 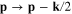 we rewrite formula (128) in the form
we rewrite formula (128) in the form

By changing the integration variable 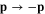 we rewrite expression (129) as follows
we rewrite expression (129) as follows

Because both E(p) and n(p) are the function of p2, we have
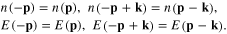
Therefore
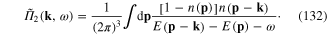
By means of the substitution  we obtain
we obtain
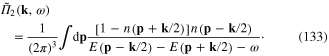
Combining (130) and (133), finally we derive the expression of 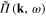
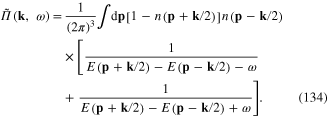
Consider the case of the electron gas at vanishing absolute temperature T = 0 and denote pF the magnitude of the momentum of electrons at the Fermi surface. Because n(p) is equal to unity inside and on the Fermi surface, i. e. at 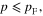 and vanishes outside this surface, i. e. at
and vanishes outside this surface, i. e. at 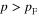 , the domain of integration in the rhs of formula (1134) must be the common region of the volume inside the spherical surface
, the domain of integration in the rhs of formula (1134) must be the common region of the volume inside the spherical surface  and the region outside the spherical surface
and the region outside the spherical surface 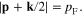 At small values of k
At small values of k 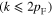 two spheres
two spheres 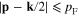 and
and 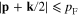 are overlapping (figure 1) and the domain of integration is the region bounded by two above-mentioned spherical surfaces.
are overlapping (figure 1) and the domain of integration is the region bounded by two above-mentioned spherical surfaces.
Figure 1. The integration domain Ω is confined inside the region with the yellow color [32]. 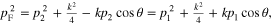

Download figure:
Standard image High-resolution imageLet us choose the direction of vector k to be that of the vertical axis Oz in the rectangular coordinate system. Then for small values of k, the domain of integration is the region bounded from above by the spherical surface  and bounded from below by the spherical surface
and bounded from below by the spherical surface 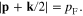 In this case formula (134) becomes
In this case formula (134) becomes
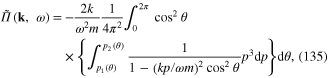
where
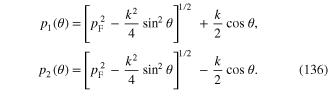
Expanding the rhs of formula (135) into the power series of the small variable k2 and limiting at the second order approximation, we obtain
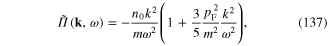
where

is the electron density. Substituting expression (137) into the rhs of formula (123), using formula (125) and setting
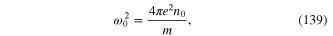
we obtain
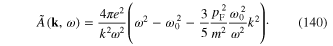
Finally we consider the dynamical equation (119). In this case kernel 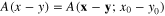 has the form (122) with the Fourier transform (123) determined by formula (140). Introducing the Fourier transformation of the scalar field
has the form (122) with the Fourier transform (123) determined by formula (140). Introducing the Fourier transformation of the scalar field 
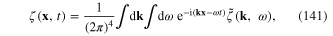
we can rewrite the dynamical equation (119) as follows
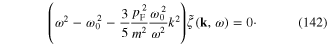
Therefore between the energy ω and the momentum k of the free plasmon we have following dispersion equation
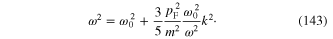
In the first-order approximation with respect to the small ratio  this dispersion equation has the following solution
this dispersion equation has the following solution
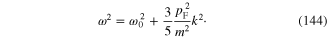
In this approximation the Fourier transform  of the kernel of the dynamical equation for free plasmon has the expression
of the kernel of the dynamical equation for free plasmon has the expression
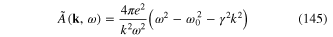
with
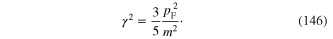
Note that the dispersion formula (144) was previously by many authors in conventional theory of plasma oscillations [37, 38]. The agreement of the above-presented result with that of the conventional theory of plasma oscillation demonstrates the validity of the functional integral method.
3.4. Quantization of plasmon field
Lets us apply the presented results to the study of the effective action (118) of the homogeneous free electron gas in the three-dimensional space. Consider the quadratic part of the this effective action
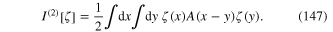
Using the Fourier transformation (122) of A(x−y) and Fourier transformation (141) of the wave function 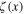 we rewrite the functional (147) in the momentum representation
we rewrite the functional (147) in the momentum representation
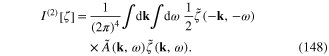
Then using expression (145) of  and setting
and setting
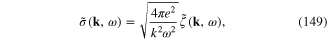
we obtain the expression of the functional (148) in terms of the new function 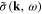
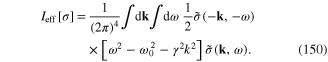
Considering 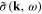 as the Fourier transforms of a new scalar field
as the Fourier transforms of a new scalar field 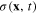
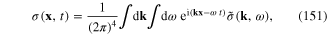
we obtain the following formula for the effective action of this new scalar field
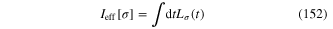
with the effective Lagrangian
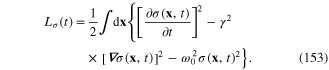
It is straightforward to derive the Lagrange equation of this scalar field
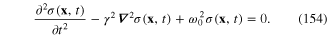
It follows that between the frequency ω and the wave vector k of the plane waves of the scalar field  there must exist the relation
there must exist the relation
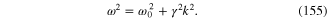
Finally we perform the quantization of the scalar field in the framework of the canonical quantization procedure. The canonical momentum 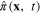 corresponding to the canonical coordinate
corresponding to the canonical coordinate 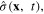 by definition, is the operator
by definition, is the operator
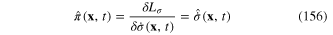
with the notation

The Hamiltonian of the system has the expression

According to the canonical quantization rule, between operators 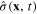 and
and 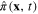 there exist the following equal-time commutation relations
there exist the following equal-time commutation relations
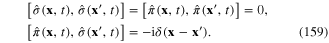
The expressions (153) and (158) for the Lagrangian and the Hamiltonian of the new scalar field 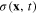 look like those of the Klein–Gordon real (hermitian) scalar field in relativistic quantum field theory except for scaling factor γ of the spatial coordinates. For the interpretation of the physical meaning of this scalar field we can apply the reasonning of the relativistic quantum field theory. In order to simplify the presentation we quantize the scalar field
look like those of the Klein–Gordon real (hermitian) scalar field in relativistic quantum field theory except for scaling factor γ of the spatial coordinates. For the interpretation of the physical meaning of this scalar field we can apply the reasonning of the relativistic quantum field theory. In order to simplify the presentation we quantize the scalar field 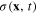 in a cubic box with a very large volume V, using the periodic boundary conditions, and expand the scalar field
in a cubic box with a very large volume V, using the periodic boundary conditions, and expand the scalar field 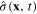 as follows
as follows
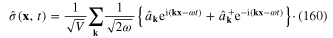
The corresponding expansion of the canonical momentum is
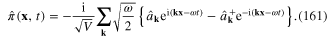
Inverting the expansions (160) and (161) to express 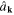 and
and 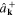 in terms of
in terms of 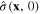 and
and  we obtain
we obtain

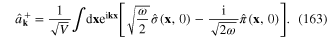
From the canonical quantization rules (159) it follows the canonical commutation relations between operators 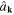 and
and  We obtain
We obtain
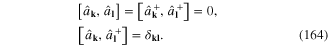
The Hamiltonian (158) is expressed in terms of these operators as follows
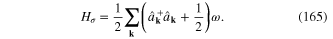
Remember that between frequency ω and wave vector k there exists the relation (155).
Operators  and
and 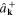 are interpreted as the destruction and creation operators of the quanta of the quantized scalar field
are interpreted as the destruction and creation operators of the quanta of the quantized scalar field 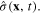 These quanta are called the plasmons, and formula (155) becomes the relation between energy and momentum of plasmon.
These quanta are called the plasmons, and formula (155) becomes the relation between energy and momentum of plasmon.
4. Plasmon–photon interaction in canonical quantum mechanics
Consider now the interaction of the electron gas with some external electromagnetic field. We choose to work in the transverse gauge of the electromagnetic field and denote 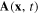 its vector potential
its vector potential
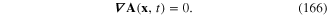
It was known [39] that the interaction Lagrangian has the following expression
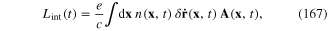
where c is the light velocity in the vacuum. Using relation (1) between the electron density 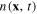 and the charge density
and the charge density  of the electron gas, we rewrite the expression in the rhs of equation (167) as follows
of the electron gas, we rewrite the expression in the rhs of equation (167) as follows
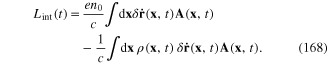
In section 2 we have established the relationship between 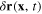 and the plasmonic field
and the plasmonic field  Therefore in order to study the plasmon–photon interaction it is necessary to express
Therefore in order to study the plasmon–photon interaction it is necessary to express 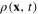 in term of the components of the vector
in term of the components of the vector 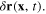 For this purpose we use formula (12), a consequence of the conservation of the total electron number in the electron gas. Using relation (1), we derive the following differential equation for the function
For this purpose we use formula (12), a consequence of the conservation of the total electron number in the electron gas. Using relation (1), we derive the following differential equation for the function 
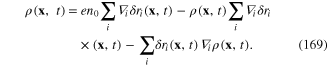
Since this differential equation cannot be exactly solved, we look for 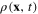 in the form of a functional power series of the components
in the form of a functional power series of the components  and write the solution in the form
and write the solution in the form
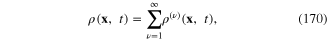
where 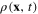 is the term of the ν-th order with respect to the components
is the term of the ν-th order with respect to the components 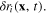 Let us limit to the third order. By means of standard calculations it can be shown that
Let us limit to the third order. By means of standard calculations it can be shown that
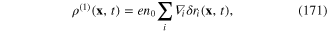
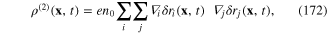
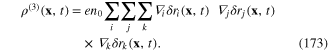
Substituting expression (170)–(173) into the rhs of relation (168), we obtain the explicit expression of the interaction Lagrangian Lint(t) in term of the components 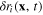
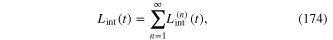
where up to the fourth order we have
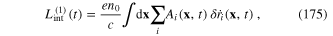
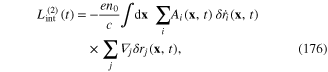

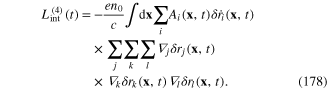
In order to derive the relation between components  and the plasmonic field
and the plasmonic field 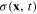 we use formula (15) with the longitudinal
we use formula (15) with the longitudinal 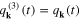 but without the transverse ones
but without the transverse ones
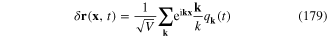
as well as relation (29) between the generalized coordinate 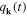 and the Fourier component
and the Fourier component 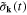 of the plasmonic field
of the plasmonic field 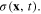 Thus we have
Thus we have
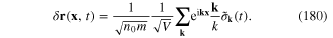
Expressing the Fourier component 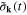 of the plasmonic field
of the plasmonic field 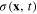 in terms of this field
in terms of this field
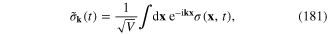
from equation (180) we obtain
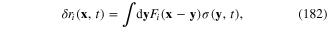
where
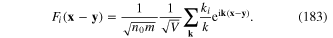
Vector function F(x−y) with components (183) can be called the characteristic function or characteristic factor of the plasmon. Substituting expression (182) of the components 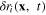 into the rhs of relations (175)–(178), finally we obtain
into the rhs of relations (175)–(178), finally we obtain
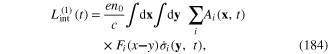
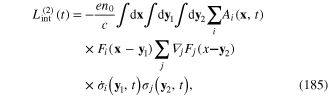
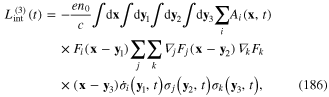
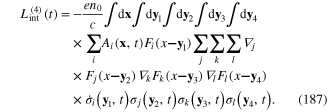
These formulae show that the interaction processes are nonlocal. The physical origin of this nonlocality is the complex structure of plasmon. Each plasmon is not a point particle, but it has the spatial extension around its center.
The plasmon–photon interaction Lagrangian (174) with the terms of the form (175)–(178) was derived when we use the electron–photon interaction Lagrangian (167) which is linear with respect to the vector potential A(x, t). If the nonlinear optical processes are taken into account, the electron–photon interaction Lagrangian must include also the terms nonlinear with respect to A(x, t). In this case the plasmon-photon interaction Lagrangian contains nonlinear terms describing the interaction processes with the participation of many photons.
5. Plasmon–photon interaction in functional integral technique
The most powerful tool for the theoretical study of plasmonic processes and phenomena is the functional integral technique. In order to apply this technique to the study of plasmon–photon interaction let us extend the reasoning presented in section 3 and substitute
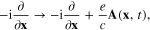
e being the absolute value of the electron charge, in the expression (62) of the quantum mechanical Hamiltonian of the electron. Then instead of the functional integral Z of the plasmonic field defined by formula (94) we must start from following functional integral of the electron gas interacting with some external transverse electromagnetic field A(x):
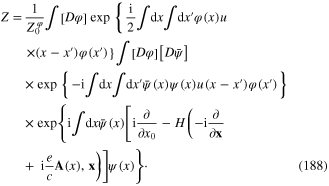
Then instead of formulae (95), (96), (105) and (106) we have following expression
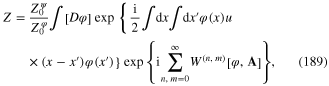
where
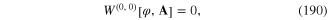
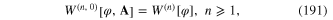
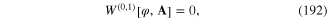
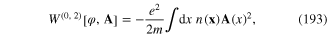
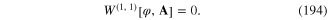
![${{W}^{(n)}}\left[ \varphi \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn177.gif) with n = 1, 2 and 3 were given in formulae (100), (102) and (104). In general,
with n = 1, 2 and 3 were given in formulae (100), (102) and (104). In general, ![${{W}^{(n,m)}}\left[ \varphi ,{\bf A} \right]$](https://content.cld.iop.org/journals/2043-6262/6/2/023001/revision1/ansn508102ieqn178.gif) is a homogenerous functional of the nth order with respect to the field φ(x) and of the mth order with respect to the field A(x). For example
is a homogenerous functional of the nth order with respect to the field φ(x) and of the mth order with respect to the field A(x). For example
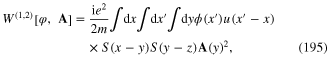
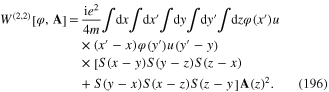
The scalar field φ(x) is expressed in terms of the plasmonic field σ(x,t) by means of formulae (117), (141), (149) and (151).
Thus the effective action

of the interaction between the scalar plasmonic field σ(x, t) and the transverse electromagnetic field A(x, t) has been established. It shows that this interaction is nonlocal. Moreover, it is not instantaneous. From the above-presented formulae it is straightforward to derive the effective action corresponding to any plasmon–photon coupling vertex such as:
- -photon absorption or emission by a plasmon (n = 2, m = 1),
- -decay of a plasmon into two photons, stokes or anti-stokes Raman scattering with the creation or the destruction of a plasmon (n = 1, m = 2),
- -photon–plasmon scattering, annihilation of two plasmons into two photons (n = 2, m = 2) and so on. This will be done in a subsequent work.
6. Conclusion and discussions
In the present work we have reviewed the main results of the rigorous theoretical study of the plasmonic processes in the interacting electron gas. Only general basic postulates (axioms), called also the first principles, of the quantum theory are accepted as the assumptions. Two different methods were applied: the quantum-mechanical canonical quantization method and the functional integral technique. The reasonings of both methods were presented in this review.
The motivation to the research on the subject of the present review was explained in the introduction. The content of section 2 is the presentation on the quantum-mechanical canonical quantization of the plasmonic field. The functional integral method in quantum theory of plasmonic field was elaborated in section 3. The study on the plasmon–photon interaction in the quantum-mechanical canonical theory is the content of section 4. In section 5 the functional integral methods was applied to the study of the plasmonic processes.
From the results of the study by both methods we can firmly conclude that all plasmonic interaction processes in the matter are nonlocal ones, in contrast to the local interaction Hamiltonian accepted in the phenomenological theories as the assumptions. Thus it is worth revising the interaction Hamiltonians accepted in references [5–28], and a lot of works should be done in the future.
However, the contents of the reviewed theoretical works are still not enough for the comparison of the theoretical predictions with the experimental data, because the electron–phonon interaction certainly plays the important role in the physical processes with the participation of plasmons, but until now there was no theoretical work on related subjects. We do hope that the present review will motivate the theoretical research on the contribution of electron–phonon interaction to the plasmonic processes.
We have seen that there exist two related but different methods for the study of the plasmon–photon interacting system: the canonical quantization method of quantum mechanics and the functional integral method of quantum field theory. In the simple case of the homogeneous and isotropic electron gas in bulk conducting solid the results of both methods are consistent. However, even for this simple case, in the framework of the functional integral method we can derive the formula determining the momentum dependence of the plasmon energy (the plasmon dispersion) by means of simple calculations, while in the canonical quantization method of quantum mechanics it is necessary to carry out complicated calculations of the perturbation theory and the renormalization procedure. Moreover, it is very difficult to apply the canonical quantization method of quantum mechanics to the study of many photonic processes and phenomena, while the functional integral technique is a very efficient theoretical tool for the study of all plasmonic processes and phenomena as well as the plasmonic devices and systems.
Acknowledgment
The authors would like to express their deep gratitude to the Advanced Center of Physics and Institute of Materials Science, Vietnam Academy of Science and technology for the support.


