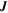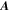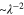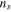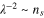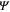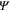Abstract
We begin with an introduction of superconductivity by giving a brief history of the phenomenon. The phenomenological Ginzburg–Landau theory and the microscopic theory of Bardeen, Cooper and Schrieffer are outlined. In view of recently available multi-band superconductors, relevant theories of both types are discussed. Unlike the traditional GL theory an extended GL theory is developed relevant to temperatures below the critical temperature. Superconductivity in a nanosystem is the highlight of the remaining part of the paper. Theories and experiments are discussed to give an interested reader an updated account and overview of what is new in this active area of research.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction (with a brief history)
Superconductivity is an unanticipated phenomenon, which has a fascinating history in the realm of quantum science. The surprising fact that certain materials below a critical temperature completely lose their electrical resistance and at the same time repel a magnet, remained a mystery until a microscopic explanation became available in 1957 nearly five decades after its discovery. During these five decades there were many attempts to understand superconductivity both theoretically and experimentally. Two important phenomenological theories are mentioned here.
- (i)A successful phenomenological theory [1] was proposed in 1935 by the London brothers, Fritz and Heinz. It is a macroscopically correct theory to treat electrodynamical aspects. They showed that the current density
 in a superconductor is proportional to the magnetic vector potential
in a superconductor is proportional to the magnetic vector potential  . The proportionality constant is
. The proportionality constant is  , where
, where  is the magnetic penetration depth, one of the characteristic lengths of a superconductor. It relates to the superfluid density
is the magnetic penetration depth, one of the characteristic lengths of a superconductor. It relates to the superfluid density  , as
, as  . The London brothers' theory both implies zero resistance and leads to a consistent explanation of the Meissner effect (repulsion of the magnetic field).
. The London brothers' theory both implies zero resistance and leads to a consistent explanation of the Meissner effect (repulsion of the magnetic field). - (ii)In 1950 Ginzburg and Landau (GL) gave their celebrated phenomenological theory of superconductivity [2]. The GL theory, also known as
 theory, proposes an order parameter
theory, proposes an order parameter  which encodes the nature of superconductivity through the symmetry of the system. To this day the GL theory remains a powerful practical tool that succinctly explains all the thermo- and electrodynamical properties. It also leads to a second fundamentally significant length
which encodes the nature of superconductivity through the symmetry of the system. To this day the GL theory remains a powerful practical tool that succinctly explains all the thermo- and electrodynamical properties. It also leads to a second fundamentally significant length  , the coherence length describing the spatial scale over which the order parameter varies.
, the coherence length describing the spatial scale over which the order parameter varies.
In terms of these two characteristic lengths GL defined a quantity 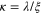 .
.  identifies the type of superconductivity (Type I or Type II) from the relation
identifies the type of superconductivity (Type I or Type II) from the relation 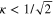 or
or 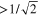 . This important relation signifies whether the surface free energy of a superconductor is positive or negative implying the magnetic field to be completely expelled from the superconductor (Meissner effect) or the magnetic field can be allowed in the superconductor as quantized vortices, respectively. For Type II superconductors, increasing the magnetic field causes the vortices to form a spatially ordered structure of vortex rods parallel to the magnetic field, known as an Abrikosov lattice [3]. Abrikosov's work was based on the solution of GL equations in presence of a magnetic field.
. This important relation signifies whether the surface free energy of a superconductor is positive or negative implying the magnetic field to be completely expelled from the superconductor (Meissner effect) or the magnetic field can be allowed in the superconductor as quantized vortices, respectively. For Type II superconductors, increasing the magnetic field causes the vortices to form a spatially ordered structure of vortex rods parallel to the magnetic field, known as an Abrikosov lattice [3]. Abrikosov's work was based on the solution of GL equations in presence of a magnetic field.
In 1950 two American groups observed the isotope effect that suggest that the transition temperature, 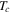 , changes inversely as the isotopic mass
, changes inversely as the isotopic mass 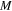 , namely
, namely 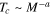 , where
, where 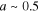 . This is strong evidence to invoke electron–phonon interaction in the theory of superconductivity as suggested by Fröhlich. In 1955 Bardeen and Pines [4] studied the nature of dielectric screening in a metal and there was a strong indication that, near the Fermi surface, the dynamics of the dielectric function can change the net interaction between two electrons to be effectively attractive. This happens when the dynamically screened Coulomb interaction is overcome by the electron–phonon interaction, which creates a local distortion of the positive-ion lattice in resonance with the electronic motion.
. This is strong evidence to invoke electron–phonon interaction in the theory of superconductivity as suggested by Fröhlich. In 1955 Bardeen and Pines [4] studied the nature of dielectric screening in a metal and there was a strong indication that, near the Fermi surface, the dynamics of the dielectric function can change the net interaction between two electrons to be effectively attractive. This happens when the dynamically screened Coulomb interaction is overcome by the electron–phonon interaction, which creates a local distortion of the positive-ion lattice in resonance with the electronic motion.
On this background Bardeen has a strong conviction that an electron pair near the Fermi surface can be bound by an attractive potential, which was confirmed cleverly by Cooper in 1956 [5]. He showed that a normal Fermi liquid in the presence of even the weakest attractive force close to the Fermi surface leads to an isolated bound state pair with a discrete negative energy relative to the Fermi energy. The components of the pair retain their Fermi velocities, yet the pair as a quantized entity has zero total momentum and zero total spin. With no loss of time Bardeen, Cooper and Schrieffer [6] formulated what would happen when many such pair states near the Fermi surface undergo a fermionic condensation. By this a new ground state is generated separated from the normal ground state by an energy gap, 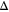 . This is the celebrated BCS theory, considered as the standard model for metallic superconductors. It successfully explains at least qualitatively a host of experimental findings and predicts many new superconducting properties. This theory explained almost all known properties of superconductors: excited states, specific heat, critical magnetic fields, ultrasonic attenuation, Meissner effect, penetration depth etc. Besides these, it predicted
. This is the celebrated BCS theory, considered as the standard model for metallic superconductors. It successfully explains at least qualitatively a host of experimental findings and predicts many new superconducting properties. This theory explained almost all known properties of superconductors: excited states, specific heat, critical magnetic fields, ultrasonic attenuation, Meissner effect, penetration depth etc. Besides these, it predicted 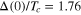 , the specific heat jump at
, the specific heat jump at 
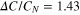 , the magnitude of the gap
, the magnitude of the gap 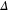 , dependent on the strength of attractive interaction and many others.
, dependent on the strength of attractive interaction and many others.
Soon after the discovery Anderson [7] noted that the central character of superconductivity extends well beyond the domain of the BCS theory itself. He raised more fundamental issues such as broken gauge symmetry, which was further investigated by Nambu in 1960 [8]. Clarification of pairing mechanism and the simplification of its derivation was given in 1958 independently by Bogolyubov [9] and Valatin [10].
We noted above that the GL theory is our best phenomenological theory with many advantages for working out the real properties of inhomogeneous superconducting materials. This theory is also used in a variety of problems in other areas of physics, namely high energy physics, gauge theory, nonlinear optics and others.
1.1. GL theory derivable from BCS
In 1958 Gor'kov reformulated the BCS theory of superconductivity in the language of quantum field theory [11]. Soon after, Gor'kov made an important contribution to relate phenomenological GL theory with the microscopic BCS within some limitations. We present here briefly the equivalence.
1.1.1. GL theory
In GL theory the free energy density, f of a superconductor near the normal to superconductive transition is expressed in terms of a complex order parameter (field) 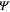 , which is nonzero below
, which is nonzero below 
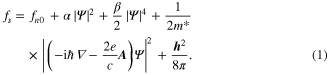
Here  and
and  are two phenomenological parameters.
are two phenomenological parameters.  is
is 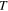 -dependent and chosen in the form
-dependent and chosen in the form 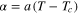 .
. 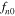 is the normal state free energy density,
is the normal state free energy density, 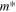 is the effective mass and
is the effective mass and  is the charge of an electron.
is the charge of an electron. 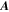 is the magnetic vector potential given by
is the magnetic vector potential given by  ,
, 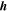 being the magnetic field. By varying the free energy with respect to
being the magnetic field. By varying the free energy with respect to  and
and 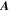 , one obtains two GL equations
, one obtains two GL equations
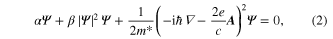
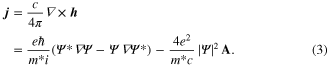
Here 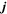 is the current density. Solution of these two equations (with appropriate boundary conditions) determines the order parameter and the current density.
is the current density. Solution of these two equations (with appropriate boundary conditions) determines the order parameter and the current density.
For a homogeneous superconductor the first GL equation gives  for
for  . It is a nontrivial solution typical for a second-order transition.
. It is a nontrivial solution typical for a second-order transition.
For non-zero magnetic field and non-zero gradient of 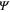 , one can calculate the characteristic lengths
, one can calculate the characteristic lengths 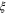 (coherence length) and
(coherence length) and 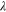 (penetration depth), as mentioned earlier. Here it is noted that the basis of the theory rests on two approximations correct around the critical temperature
(penetration depth), as mentioned earlier. Here it is noted that the basis of the theory rests on two approximations correct around the critical temperature 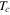 . The order parameter
. The order parameter 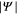 is small near
is small near 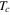 and
and 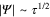 where
where 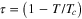 . Despite these limitations there is a myth that the GL theory applies not only around
. Despite these limitations there is a myth that the GL theory applies not only around  , rather it is useful for very low temperature. More in the next section.
, rather it is useful for very low temperature. More in the next section.
1.1.2. BCS theory
It is developed with an assumption that there is an attractive interaction between a pair of electrons by the mediation of a phonon in conventional metallic systems. The theory can be generalised such that any boson can mediate the interaction to produce a bound pair. The many body reduced Hamiltonian is written as
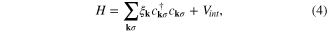
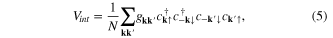
where 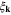 is the electron excitation energy,
is the electron excitation energy, 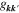 is the pairing interaction involving
is the pairing interaction involving  and
and 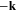 and
and 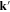 and
and 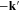 with up and down spins, respectively. Using any one of the techniques (BCS variational method, Bogolyubov–Valatin canonical transformation, Bogolyubov–de Gennes approach or Gor'kov's thermodynamic Green functions) we obtain the BCS gap equation using the definition
with up and down spins, respectively. Using any one of the techniques (BCS variational method, Bogolyubov–Valatin canonical transformation, Bogolyubov–de Gennes approach or Gor'kov's thermodynamic Green functions) we obtain the BCS gap equation using the definition

After going through some algebra [12–14], at 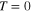 one obtains the gap equation
one obtains the gap equation
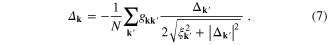
Assuming 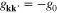 for
for 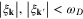 (Debye cut-off), the k-independent gap equation is
(Debye cut-off), the k-independent gap equation is

If the density of states near 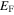 is nearly constant within
is nearly constant within 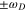 , the gap is given by
, the gap is given by
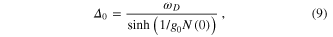
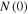 is the density of states at the Fermi energy. In the weak-coupling case
is the density of states at the Fermi energy. In the weak-coupling case 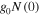 being small, the gap is now
being small, the gap is now
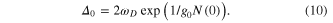
At finite temperature, this equation is
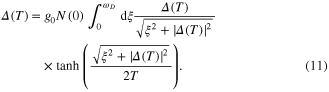
1.1.3. Equivalence of GL with BCS near Tc
Following Gor'kov [13] one can obtain after some algebra the following equation
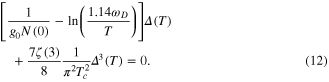
Near Tc the coefficient of  may be expanded as
may be expanded as 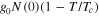 , then in the uniform limit (
, then in the uniform limit (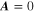 ), the order parameter
), the order parameter 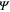 is proportional to
is proportional to  . The final results are
. The final results are
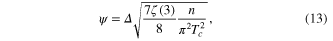
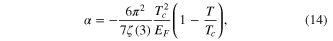

 is the electron density. Here we presented the order parameter
is the electron density. Here we presented the order parameter 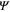 proportional to the energy gap
proportional to the energy gap 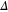 of the BCS theory and the coefficients
of the BCS theory and the coefficients  and
and 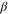 of GL theory in terms of physical parameters
of GL theory in terms of physical parameters 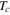 ,
, 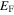 and
and  . In view of these results the GL theory is almost complete in a limited sense, which is correct near
. In view of these results the GL theory is almost complete in a limited sense, which is correct near 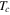 . We are reminded that
. We are reminded that 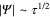 , where
, where 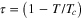 . Here we have a clear understanding that the GL theory is just not phenomenological, rather it has a microscopic basis as discussed above.
. Here we have a clear understanding that the GL theory is just not phenomenological, rather it has a microscopic basis as discussed above.
Before we proceed further we give an outline of the rest of the paper. Novel superconductors, particularly the multiband (gap) ones are covered in section 2. We present GL theory, BCS theory and GL theory derivable from the BCS. In section 3 we discuss further expansion as mentioned above to include higher power of 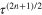 (
(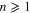 ) and their interesting consequences. We present some selected results on the gaps (both single and multiband materials) from our published calculations. In section 4 we discuss some current activity in nano-superconductors based on both BCS and GL theories. There have been many interesting reports on the novelty of nano-superconductors. This is a new area that is coming up vigorously. We present a balanced review of what confinement does to the smallness of nano-superconductors. Section 5 gives a brief summary and conclusions.
) and their interesting consequences. We present some selected results on the gaps (both single and multiband materials) from our published calculations. In section 4 we discuss some current activity in nano-superconductors based on both BCS and GL theories. There have been many interesting reports on the novelty of nano-superconductors. This is a new area that is coming up vigorously. We present a balanced review of what confinement does to the smallness of nano-superconductors. Section 5 gives a brief summary and conclusions.
2. Multiband superconductors
The electronic structure of real materials is much more complicated in comparison to the simple jellium model that was adopted in the original BCS theory. If we examine the band structure of superconducting materials, in most of them the Fermi energy passes through many bands and hence the Fermi surfaces are multi-sheeted with the same or different energy gap amplitudes. Evidence of two energy gaps are even obtained in high purity elemental superconductors, for example Nb, Ta and V [15], Nb doped SrTiO3 [16]. More recently, multiband superconductivity involving 2 to 5 bands with more complicated Fermi surfaces are observed in a variety of novel superconductors, such as MgB2 [17–19], RNi2B2C (R = Lu, Y) [20] and FeAs family of superconductors [21]. A variety of experiments are reported, namely magnetisation, transport, specific heat, penetration depth, tunnelling, photo-electron spectroscopy, small angle neutron scattering etc, where multiple gaps are easily inferred.
Soon after the BCS theory appeared, Suhl et al [22] and Moskalenko [23] independently extended the one band BCS theory to two bands with overlapping energy bands at the Fermi surface. The two band theory was further discussed by Kondo [24], where the solutions are obtained by using Bogolyubov's variational method. Tilley [25] obtained these results by using Gor'kov's Green function technique. Additionally, Tilley derived GL equations for the two band case from the BCS method following the one band equivalence as mentioned above due to Gor'kov. The two-band model has been explored intensely starting with the work of Geilikman et al [26]. Many other authors used this model in the context of high  oxides [27] and MgB2 [28–32]. Brandt and Das [33] have presented a comprehensive review of the latter topic.
oxides [27] and MgB2 [28–32]. Brandt and Das [33] have presented a comprehensive review of the latter topic.
2.1. Multiband GL theory
Multiband GL theory can be seen as a straight forward generalisation of the standard GL theory. The free energy density can be expanded as powers of multi-order parameters [34, 35]. Here one has total superconducting free energy composed of individual parts and mutual interaction terms arising out of various order parameters and gradient terms. Here we consider the case of two order parameters. Generalization to multi-order parameters is a straight forward case. The simplest inter-order parameter coupling is the internal Josephson coupling term that we consider below. The free energy density is written as
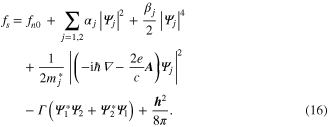
Here the last but one term is the Josephson coupling term, with interaction strength  . Let us consider the applied field is zero and we are in the bulk at the temperature
. Let us consider the applied field is zero and we are in the bulk at the temperature 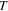 close to
close to 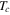 . By neglecting the
. By neglecting the 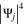 term, the free energy density (with reference to normal state) is given by
term, the free energy density (with reference to normal state) is given by
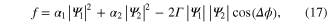
where 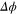 is the phase difference between two condensates.
is the phase difference between two condensates.
When 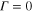 two bands are fully decoupled and two order parameters have two critical temperatures. For
two bands are fully decoupled and two order parameters have two critical temperatures. For  the free energy is minimized with
the free energy is minimized with  . For
. For 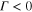 the free energy is stable with
the free energy is stable with 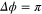 . This implies the condensation energy for two-band superconductivity is more stable than the two independent states. More on two-band nanosystems in section 4.f.i.
. This implies the condensation energy for two-band superconductivity is more stable than the two independent states. More on two-band nanosystems in section 4.f.i.
The GL equations for 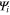 are obtained from the minimization of the free energy and similarly the equation for the current. The self-consistent solutions of these (
are obtained from the minimization of the free energy and similarly the equation for the current. The self-consistent solutions of these (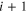 ) equations describe the properties of multiband superconductors within the traditional GL theory (see [27–35]).
) equations describe the properties of multiband superconductors within the traditional GL theory (see [27–35]).
In the recent past it has been argued [28, 36–40] that the original GL theory is incomplete beyond the order parameter  . Therefore, one has to incorporate the higher order terms (
. Therefore, one has to incorporate the higher order terms (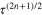 for
for  ) as a systematic expansion, see Fetter and Walecka [41]. For the derivation of this result one has to expand the order parameter equation in powers of
) as a systematic expansion, see Fetter and Walecka [41]. For the derivation of this result one has to expand the order parameter equation in powers of 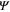 and its spatial gradients. Details of this theory are in our recent paper [40].
and its spatial gradients. Details of this theory are in our recent paper [40].
2.2. Multiband BCS theory
One band theory is generalised to a multiband [22, 23] situation. For simplicity we consider a two-band case. Multiband generalization is straightforward
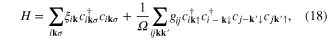
here 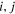 stand for the band indices 1, 2.
stand for the band indices 1, 2. 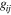 is the intra- and interband couplings, and
is the intra- and interband couplings, and 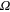 is the volume.
is the volume.
Using the same variational principle as in the one-band case, the gap equation is
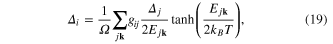
where  .
.
Explicitly, two gaps are given by
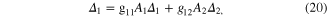

where
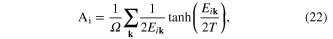
gij are interaction matrix involving diagonal 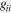 and off-diagonal
and off-diagonal 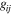 parameters related to bands
parameters related to bands 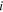 and
and 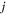 . The equation for
. The equation for 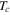 as largest
as largest 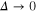 ,
,  , where
, where 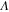 is the largest eigenvalue of
is the largest eigenvalue of 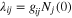

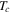 of the two band system is enhanced by the second term of the equation below
of the two band system is enhanced by the second term of the equation below

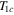 is the critical temperature for band 1.
is the critical temperature for band 1.
2.3. GL derived from BCS
As we have done in the one-band case (uniform without gradient and 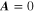 ), we follow the similar procedure in the two-band case. Self-consistency condition through third order in
), we follow the similar procedure in the two-band case. Self-consistency condition through third order in 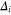 gives the same equation as in the one-band case. Near
gives the same equation as in the one-band case. Near 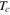 the coefficient of
the coefficient of 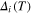 may be expanded to lowest order in
may be expanded to lowest order in  . Now by comparing the first GL equation, the values of
. Now by comparing the first GL equation, the values of 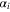 and
and 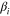 can be obtained.
can be obtained. 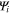 is proportional to
is proportional to 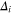 . Results are [40]
. Results are [40]
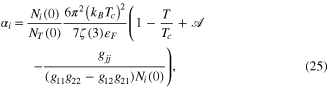
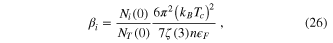
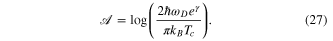
3. Beyond the standard GL theory
This is an important development in recent works on the GL theory. It is an extended version beyond the traditional GL theory [2]. Traditional GLT includes terms beyond 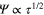 which are incomplete. One is inclined to extend it to complete the terms
which are incomplete. One is inclined to extend it to complete the terms  as done in [37–40] by which one improves the gap and other properties to lower temperatures. To accomplish the extended theory
as done in [37–40] by which one improves the gap and other properties to lower temperatures. To accomplish the extended theory 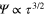 and beyond, one follows Gor'kov (see also Fetter and Walecka [41]) by expanding the self-consistent gap equation in powers of the order parameter and its spatial gradients to high orders. Depending on the desired precision the expansion terminates at some order. Details of this theory can be found in [40]. We present here some results.
and beyond, one follows Gor'kov (see also Fetter and Walecka [41]) by expanding the self-consistent gap equation in powers of the order parameter and its spatial gradients to high orders. Depending on the desired precision the expansion terminates at some order. Details of this theory can be found in [40]. We present here some results.
In figure 1(a) the energy gap 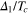 for one-band superconductor is shown as a function of temperature
for one-band superconductor is shown as a function of temperature 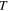 in the BCS and GL theory. The black dots are BCS results. The solid red line overshoots the BCS in the traditional GL theory, which refers to
in the BCS and GL theory. The black dots are BCS results. The solid red line overshoots the BCS in the traditional GL theory, which refers to 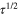 in the expansion
in the expansion 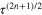 terms, which means
terms, which means  . For
. For  are shown as higher order corrections in the extended GL. The inset is a close-up of the region near
are shown as higher order corrections in the extended GL. The inset is a close-up of the region near  . It is clear that the traditional GL result is unreliable away from
. It is clear that the traditional GL result is unreliable away from  . In figure 1(b) the magnitude of individual terms is shown on a Log plot. More in the figure caption. (reference [40]).
. In figure 1(b) the magnitude of individual terms is shown on a Log plot. More in the figure caption. (reference [40]).
Figure 1. (a) The extended GL expansion is compared to a numerical full BCS result. The extended GL converges to the true solution in the region 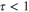 and for moderate
and for moderate  it converges quickly to that of the BCS. Inset: a close up of the region near
it converges quickly to that of the BCS. Inset: a close up of the region near 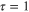 . There are singularities in the BCS function infinitesimally close to
. There are singularities in the BCS function infinitesimally close to 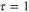 , which prevent extended GL from converging at this point. (b) The magnitude of individual terms in the extended GL expansion are shown on a Log plot. The magnitude of higher terms decays quickly except near the point
, which prevent extended GL from converging at this point. (b) The magnitude of individual terms in the extended GL expansion are shown on a Log plot. The magnitude of higher terms decays quickly except near the point 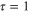 , where it remains finite. It shows the expansion is converging in the region
, where it remains finite. It shows the expansion is converging in the region 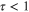 (from [40]).
(from [40]).
Download figure:
Standard image High-resolution imageNow we discuss the two-band situation. Firstly, we plot the BCS solution for both the gaps with a range of values of inter-band couplings 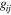 . The values of
. The values of 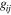 chosen are 0.001, 0.01, 0.1 and 0.55. Other parameters are in the figure caption. In figure 2(a) the energy gap for the first band is shown as a function of
chosen are 0.001, 0.01, 0.1 and 0.55. Other parameters are in the figure caption. In figure 2(a) the energy gap for the first band is shown as a function of 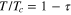 , where the inter-band coupling has a weak effect on the first gap. Nothing spectacular is seen in the first gap results. In (b) the second gap is shown for the same couplings and their effect is drastic for weaker coupling. For
, where the inter-band coupling has a weak effect on the first gap. Nothing spectacular is seen in the first gap results. In (b) the second gap is shown for the same couplings and their effect is drastic for weaker coupling. For  the second critical temperature
the second critical temperature 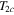 is
is 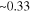 in the scale of
in the scale of 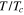 . The second gap
. The second gap 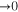 at this
at this 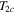 . As the couplings increase the second band has induced superconductivity from the first band and it results in the plots shown. At higher couplings the plot is reminiscent of a one-band BCS result.
. As the couplings increase the second band has induced superconductivity from the first band and it results in the plots shown. At higher couplings the plot is reminiscent of a one-band BCS result.
Figure 2. (a) and (b) are BCS gaps for first and second bands. They are compared with high expansion ( ) in the extended GL theory in (c) and (d), respectively. The parameters used here are
) in the extended GL theory in (c) and (d), respectively. The parameters used here are 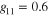 ,
, 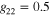 ,
, 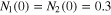 and
and 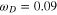 . (From [40]).
. (From [40]).
Download figure:
Standard image High-resolution imageIn figures 2(c) and (d) we show order parameters 1 and 2 calculated by using the extended GL formalism using the same parameters. For 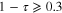 the behaviour of the GL plots is similar to that of BCS. However, for
the behaviour of the GL plots is similar to that of BCS. However, for 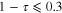 the behaviour of the order parameters is drastically different in comparison to BCS in (a) and (b), respectively. The point where the plots begin to disagree is close to the location of
the behaviour of the order parameters is drastically different in comparison to BCS in (a) and (b), respectively. The point where the plots begin to disagree is close to the location of 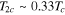 . Komendova et al [42] have argued that there is a possibility of hidden criticality near
. Komendova et al [42] have argued that there is a possibility of hidden criticality near  , which becomes critical in the limit of vanishing inter-band coupling. This feature is likely to be associated with the anomalous behaviour of the gap near this
, which becomes critical in the limit of vanishing inter-band coupling. This feature is likely to be associated with the anomalous behaviour of the gap near this  . Although the BCS solution of the first band showed only a weak perturbation with the inter-band coupling, the nonconvergent behaviour seen in the GL solution of the second band affects the dominant band drastically at lower temperature.
. Although the BCS solution of the first band showed only a weak perturbation with the inter-band coupling, the nonconvergent behaviour seen in the GL solution of the second band affects the dominant band drastically at lower temperature.
Now we consider a range of real materials FeSe0.94 [43], OsB2 [44], LiFeAs[45] and MgB2 [46]. The parameters used for these calculations are representative of the behaviour of the materials, though the exact choice is not claimed to be unique. For each set of parameters we plot the BCS and extended GL gaps with the terms in the GL calculations retained to order 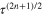 with
with 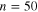 . These results are shown in figure 3. For details see [40].
. These results are shown in figure 3. For details see [40].
Figure 3. Extended GL calculations compared to full multiband BCS results. The materials are (a) FeSe0.94, (b) OsB2, (c) LiFeAs and (d) MgB2.(From [40]).
Download figure:
Standard image High-resolution imageSimilar to two-band results we also calculate for three-band materials using both extended GL and BCS theories (figure 4). The legend shows the BCS by black dots and other symbols are for extended GL with different powers of  as indicated before.
as indicated before.  for all three bands,
for all three bands,  ,
, 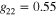 ,
, 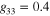 ,
,  and four columns are for
and four columns are for 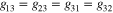 for the values 0.001, 0.01, 0.1 and 0.5, respectively.
for the values 0.001, 0.01, 0.1 and 0.5, respectively.
Figure 4. Extended GL and BCS results compared for three bands. (B J Wilson and M P Das unpublished).
Download figure:
Standard image High-resolution imageTo summarise this part we have clearly demonstrated the importance of τ(2n+1)/2 expansion for large n multi band superconductors. This point emphasises the weaker validity of the GL theory for lower temperatures for some materials and especially for applications with small inter-band couplings.
Now we address the next part when the material is nano in size, yet a superconductor.
4. From bulk to nano or 'nano in bulk' in a superconductor
As a definition, 'nanoscience' is the study of materials whose physical size is on the nanometre scale (in the range of 1–1000 nm). While 'nano' means precisely small, 'meso' is a broader term, being intermediate between the microscopic (molecular) and macroscopic (bulk) scale. In practice the 'mesoscopic' regime partly overlaps the 'nanoscopic' description [47].
For a superconductor it will not be inappropriate to argue 'nano in bulk' for the following reasons. We have said before that there are two characteristic length scales in a superconductor, coherence length(s) 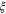 and penetration length
and penetration length 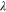 . Although a superconductor as described above may be a bulk material and superconductivity is a macroscopic quantum phenomenon, these particular and relevant length scales are nanometric in dimension. Much of interesting physics relies on these length scales when one studies the surfaces of bulk superconductors or vortices of superconductors in the presence of a magnetic field. These length scales are also meaningful for a material, whose physical size is nanometric subject to some conditions such as parity of number of electrons and fluctuations. In addition to these, the current developments in experimental nanotechnology have made nanoelectronics a very attractive subject [48, 49]. We present here some basic issues of physics including theories and experiments.
. Although a superconductor as described above may be a bulk material and superconductivity is a macroscopic quantum phenomenon, these particular and relevant length scales are nanometric in dimension. Much of interesting physics relies on these length scales when one studies the surfaces of bulk superconductors or vortices of superconductors in the presence of a magnetic field. These length scales are also meaningful for a material, whose physical size is nanometric subject to some conditions such as parity of number of electrons and fluctuations. In addition to these, the current developments in experimental nanotechnology have made nanoelectronics a very attractive subject [48, 49]. We present here some basic issues of physics including theories and experiments.
4.1. Kubo gap
In 1962, Kubo [50] proposed a theory for metallic particles, which are small in size unlike the bulk. For such systems it is only quantum mechanics that accounts for observed physical properties. In the jargon of the field, 'quantum confinement' means that the de Broglie wavelength of the particles is comparable to the size of the system that contains them. Small size implies strong quantum confinement effects. Bulk extended matter, when sufficiently curtailed in one or more of its dimensions, will behave as a quasi-two dimensional (two-DEG), a quasi-one dimensional (quantum wire) or a quasi-zero dimensional (quantum dot) system. The price to be paid for this is to lose the long-range extendedness of the wave functions. The energy of motion becomes quantized as the wave function is confined. Subject to confinement, the continuum of the density of states becomes discrete. However, the energy gaps between the states are tiny, in the meV range, if the particle size is nanometric.
Kubo recognised the inherent statistical nature of the problem. He argued the energy spectrum depends on the precise geometry of the system, even though the average energy gaps may be same. Energy spectrum in many respects leads to anomalies in the physico-chemical properties of small metallic particles at low temperatures. In brief, the Kubo gap depends on the spectrum. This gap 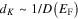 , inversely proportional to the electronic density of states at the Fermi level. Kubo gap is essentially the energy required to remove an electron from the small metal particle. See earlier reviews by Halperin [51] and von Delft and Ralph [52]. In comparison to the thermal energy, if
, inversely proportional to the electronic density of states at the Fermi level. Kubo gap is essentially the energy required to remove an electron from the small metal particle. See earlier reviews by Halperin [51] and von Delft and Ralph [52]. In comparison to the thermal energy, if 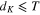 , the material is a metal and otherwise it is an insulator. Our further discussion is about only metallic nanoparticles.
, the material is a metal and otherwise it is an insulator. Our further discussion is about only metallic nanoparticles.
4.2. Anderson criterion
Following the BCS theory (meant for clean superconductors), Anderson [53] presented a theory for dirty superconductors, where the elastic scattering strength is large compared to the energy gap. Independently similar results are obtained by Abrikosov and Gor'kov [54], see also [55] for more detailed calculations. The scattering mean free path does not change the Gor'kov's anomalous Green function, which is the same as the energy gap.
Anderson's idea emphasises that often in the presence of some disorder, a superconducting state can be more stable and less likely to be suppressed [56]. This loss of superconductivity has been explored not only in nanoparticles and in nanowires, but also in more complex systems exhibiting many exciting and novel effects. For a small number of particles, as mentioned before, the allowed energy levels are quantized, discrete and the mean energy level spacing 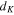 (the Kubo gap) becomes bigger for the smallness of the sample. When the superconducting energy gap
(the Kubo gap) becomes bigger for the smallness of the sample. When the superconducting energy gap 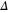 approaches
approaches 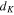 , superconductivity is suppressed at this point by the Anderson's criterion [57]. In this limit
, superconductivity is suppressed at this point by the Anderson's criterion [57]. In this limit 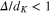 , there are no available energy levels correlated by the pairing interaction. More precisely, it has been argued [58] that superconductivity will vanish for
, there are no available energy levels correlated by the pairing interaction. More precisely, it has been argued [58] that superconductivity will vanish for 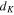 greater than a critical value
greater than a critical value 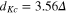 for even
for even 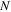 and
and  for odd
for odd 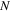 . Presently Kubo-Anderson criteria are utilised prolifically to predict superconductivity in nanosystems [59].
. Presently Kubo-Anderson criteria are utilised prolifically to predict superconductivity in nanosystems [59].
Although Anderson's criterion remained unexplored for some time, from the mid-nineties in view of many experimental investigations on nanoparticles, theoretical activities began vigorously based on the BCS reduced Hamiltonian. While the BCS theory is used for macoscopic systems, we are reminded of the Richardson solution [60], originally developed for finite nucleus. The latter approach is based on the canonical ensemble, where the number of particles is fixed. This is in contrast with the BCS theory, where grand canonical ensemble is used to deal with the macroscopic limit. While the BCS theory provides a mean-field solution, Richardson's solution is exact [61–63]. More on this in the next sub-section.
Richardson solution depends on 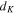 near the Fermi level
near the Fermi level 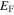 . The property of Cooper pairing depends on the 'parity' of number of electrons
. The property of Cooper pairing depends on the 'parity' of number of electrons 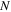 . For odd
. For odd 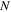 , one electron is unpaired and carries an additional energy
, one electron is unpaired and carries an additional energy 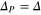 . This feature is experimentally detected [57, 64, 65] exploring the Coulomb blocked phenomenon and theoretically analysed by Matveev and Larkin [66].
. This feature is experimentally detected [57, 64, 65] exploring the Coulomb blocked phenomenon and theoretically analysed by Matveev and Larkin [66].
4.3. Theories
During the past two decades there have been a lot of activities in this area of finite size nanosuperconductors. We give here a brief review. Most of the theoretical work reported here is carried out with the BCS theory applied to a finite number of particles appropriate for nanosystems. For thin films Blatt and Thompson [66] showed the energy gap is an oscillatory as a function of film thickness passing through resonances, where the period of oscillation is the Fermi wavelength. The gap increases with a decrease of the thickness. The enhancement of superconductivity by the size effect was also discussed by Parmenter [67]. With the decrease of size the gap increases, where the weak coupling limit goes to the strong coupling case ( varies from 3.528 to 4). Thermodynamical properties, particularly specific heat, spin susceptibility of small grains are investigated in [68] by using both GL and BCS theories. Since GL is unable to deal with quasi-particles, a static approximation within the BCS was used, where contributions due to quasi particles are incorporated explicitly.
varies from 3.528 to 4). Thermodynamical properties, particularly specific heat, spin susceptibility of small grains are investigated in [68] by using both GL and BCS theories. Since GL is unable to deal with quasi-particles, a static approximation within the BCS was used, where contributions due to quasi particles are incorporated explicitly.
4.4. GL theory for nanosuperconductors
In recent years, the traditional GL theory has been applied to meso/nanosuperconductors. As mentioned earlier, it is important to apply the correct boundary conditions if the superconductivity is occurring in a small volume. On the boundary the order parameter has to vanish. On application of a magnetic field above a certain critical field a vortex can be created. The authors of this work [69] have applied traditional 3-dimensional GL theory in a parallelepiped cell containing a small mesoscopic disk at the centre. Vortex state solutions are obtained by minimising the free energy numerically by the method of simulated annealing. See reference [69] for details of calculations. The result has been shown in figure 5 as a simple example. Clearly we notice the vanishing of order parameter near the edges of the disk and at the centre where the magnetic field has penetrated.
Figure 5. Density of superconducting electrons in a disk for no vortex (Meissner state) with black filled dots and a single vortex with unfilled dots, occurring at the centre of the disk. (See [69]).
Download figure:
Standard image High-resolution imageBy using the same traditional GL theory Peeters and co-workers have studied mesoscopic superconductivity for vortex phase diagram [70]. Free energies of different vortex configurations are calculated by increasing both the disk thickness and magnetic field. The authors showed a smooth transition from a multi-vortex state to a giant vortex state (figure 6). With increment of magnetic field with steps of 0.01 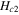 the superconductor goes from a Meissner state to vortex states as shown in the figure 6. This picture is reminiscent of formation of vortices in rotating 4He superfluid and atomic Bose–Einstein condensate [71]. In this sub-field of mesoscopic superconductors there has been plenty of theoretical and experimental activities. Some of the references are given here [72]. We also point out more recently available extended GL theory for nano/meso superconductors in the later section 4.f.ii.
the superconductor goes from a Meissner state to vortex states as shown in the figure 6. This picture is reminiscent of formation of vortices in rotating 4He superfluid and atomic Bose–Einstein condensate [71]. In this sub-field of mesoscopic superconductors there has been plenty of theoretical and experimental activities. Some of the references are given here [72]. We also point out more recently available extended GL theory for nano/meso superconductors in the later section 4.f.ii.
Figure 6. Free energy configurations with vorticity  for two disks of radius
for two disks of radius 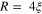 in (a) and
in (a) and 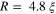 in (b),
in (b), 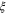 being the coherence length, is shown as a function of magnetic field
being the coherence length, is shown as a function of magnetic field 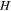 scaled by the second critical field
scaled by the second critical field 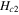 . For
. For 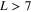 states are metastable, hence a giant vortex is formed for large
states are metastable, hence a giant vortex is formed for large 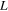 . (See [70]).
. (See [70]).
Download figure:
Standard image High-resolution image4.5. Reduced BCS Hamiltonian for nanosuperconductors
We mentioned earlier that the BCS model for bulk superconductor deals with grand canonical ensemble. For small grains it is inappropriate for use due to the fluctuations in smallness of 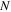 . This requires a treatment by canonical ensemble (see details in [58]). In metallic condensed systems with large N pairing occurs due to virtual exchange of phonons between the conduction electrons. In atomic nucleus with a fixed number of fermions (small N) pairing appears due to short-range nature of nuclear interaction and it includes contributions from the singlet-S and triplet-P channels. In both cases the pairs are correlated in the time-reversed states. A canonical treatment of BCS states are applied to nuclear physics soon after the former's appearance. In 1963 Richardson [60] provided an exact solution in a simplified form of the BCS, for application to nuclear physics with some more papers followed soon. Despite this, the condensed matter community did not pay much attention until the superconductivity in small metallic grains was reported in the mid-nineties [57]. Currently Richardson model is an attractive picture for nanosuperconductors.
. This requires a treatment by canonical ensemble (see details in [58]). In metallic condensed systems with large N pairing occurs due to virtual exchange of phonons between the conduction electrons. In atomic nucleus with a fixed number of fermions (small N) pairing appears due to short-range nature of nuclear interaction and it includes contributions from the singlet-S and triplet-P channels. In both cases the pairs are correlated in the time-reversed states. A canonical treatment of BCS states are applied to nuclear physics soon after the former's appearance. In 1963 Richardson [60] provided an exact solution in a simplified form of the BCS, for application to nuclear physics with some more papers followed soon. Despite this, the condensed matter community did not pay much attention until the superconductivity in small metallic grains was reported in the mid-nineties [57]. Currently Richardson model is an attractive picture for nanosuperconductors.
Richardson's reduced Hamiltonian is given by
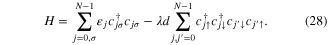
Here 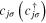 destroys (creates) electrons in free time-reversed states
destroys (creates) electrons in free time-reversed states 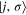 with discrete uniformly spaced degenerate eigenenergies
with discrete uniformly spaced degenerate eigenenergies  .
. 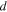 is the (Kubo)gap of the discrete spectrum,
is the (Kubo)gap of the discrete spectrum, 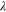 is dimensionless pairing strength. In BCS model
is dimensionless pairing strength. In BCS model 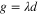 . The interaction
. The interaction 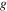 scatters only time-reversed electron pairs within the Debye cutoff frequency
scatters only time-reversed electron pairs within the Debye cutoff frequency 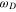 of the energy shell around the Fermi energy
of the energy shell around the Fermi energy 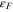 .
. 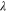 is related to the parameters bulk gap
is related to the parameters bulk gap 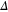 and the cutoff frequency
and the cutoff frequency  via the bulk gap equation
via the bulk gap equation 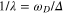 . In this model
. In this model 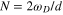 .
.
We notice here an interesting point that the nanostructure boundary condition is entering in a subtle way through the discrete spectrum. Reference [62] considers finite size corrections to the Richardson model, where the low energy spectrum of the problem is included as an expansion (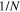 ) in the inverse of the number of electrons in the grain.
) in the inverse of the number of electrons in the grain.
Going back to the original BCS the ground state is written as
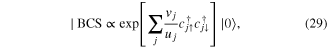
where 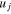 and
and 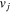 are variational parameters of the original BCS theory. These two parameters are obtained as BCS solutions from a variational minimization of the reduced Hamiltonian.
are variational parameters of the original BCS theory. These two parameters are obtained as BCS solutions from a variational minimization of the reduced Hamiltonian.
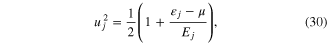
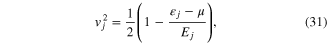
with the quasi-particle excitation energy given by ![${{E}_{j}}=\sqrt{\left. \varepsilon _{j}^{2}+{{\left| \Delta \right|}^{2}} \right]}$](https://content.cld.iop.org/journals/2043-6262/6/1/013001/revision1/ansn505364ieqn213.gif) .
. 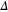 is the energy gap that we have discussed earlier. In the grand canonical ensemble this BCS ground state is asymptotically exact for
is the energy gap that we have discussed earlier. In the grand canonical ensemble this BCS ground state is asymptotically exact for 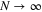 . For finite
. For finite 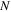 it requires a canonical ensemble, for which a projected BCS (PBCS) ansatz is used, which is given by
it requires a canonical ensemble, for which a projected BCS (PBCS) ansatz is used, which is given by
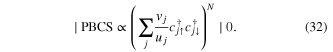
It is an 'N conserving theory' [61]. Apart from BCS and PBCS ansatz, there are other numerical approaches, namely Lanzcos method [74], perturbative renormalization group method [65] and density matrix renormalization group technique [58]. These methods have been extensively used for nanosuperconductivity. See reviews [52, 73].
For the novel physics for finite N, we have size, shape and shell effects, effects of fluctuations and odd–even parity [75–79]. Randomness of eigenvalue distributions raises new question of statistics of ensembles in the Dyson–Wigner sense. These features are in the presence of pairing correlations unlike in single-particle physics of disordered systems [80]. Thermodynamic properties of small superconducting grains are studied in detail in [81] by analytical and numerical methods. Here the authors have studied in the limit of d/Δ > 1 and the crossover of superconducting to normal grains.
An interesting point of all this important work is to emphasise how a crossover of bulk to a nanosystem is possible. Although Anderson's criterion has been in the literature for over five decades, the ground breaking experiments of Tinkham and co-workers [57] brought new light on ultra-thin nanosuperconductivity. Without going through details, a list (incomplete) gives an idea of experimental activities [59].
On the other hand, by using the BCS theory appropriate for nanosystems, namely Richardson model, it opened a new panorama in this novel area of superconductivity.
A illustrations we present here some results of calculations. In figure 7 (upper panel) calculations of condensation energy given by the difference of ground state energy of the pairing Hamiltonian and the energy of the filled Fermi state, 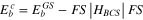 . The condensation energy is scaled by the bulk superconducting gap. They are shown for even (b = 0) and odd (b = 1) parity state in the PBCS and exact calculations. The parity effect in terms of the gap parameter is given by the difference of ground state energy of an odd grain and the mean energy of the neighbouring even grains by adding or removing an electron. This gives the Matveev–Larkin (ML) gap by the expression [65]
. The condensation energy is scaled by the bulk superconducting gap. They are shown for even (b = 0) and odd (b = 1) parity state in the PBCS and exact calculations. The parity effect in terms of the gap parameter is given by the difference of ground state energy of an odd grain and the mean energy of the neighbouring even grains by adding or removing an electron. This gives the Matveev–Larkin (ML) gap by the expression [65] ![${{\Delta }_{ML}}={{E}_{1}}\left( N \right)-1/2\left[ {{E}_{0}}\left( N+1 \right)+{{E}_{0}}\left( N-1 \right) \right]$](https://content.cld.iop.org/journals/2043-6262/6/1/013001/revision1/ansn505364ieqn218.gif) . The lower panel of figure 7 gives the ML gap scaled to the bulk gap as a function of grain size by the PBCS (dashed line) and exact (continuous line) methods. One can see the asymptotic limits of both PBCS and exact results. It is also interesting to note that the Anderson's criterion
. The lower panel of figure 7 gives the ML gap scaled to the bulk gap as a function of grain size by the PBCS (dashed line) and exact (continuous line) methods. One can see the asymptotic limits of both PBCS and exact results. It is also interesting to note that the Anderson's criterion  is satisfied. For details see [73].
is satisfied. For details see [73].
Figure 7. Upper panel shows condensation energy for ( ) and odd (
) and odd (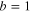 ) grains calculated using PBCS and exact wave functions as a function of grain size. The lower panel gives the Matveev–Larkin gap in PBCS and exact calculations (from [73]).
) grains calculated using PBCS and exact wave functions as a function of grain size. The lower panel gives the Matveev–Larkin gap in PBCS and exact calculations (from [73]).
Download figure:
Standard image High-resolution imageFluctuation effects are calculated in [62]. Figure 8 shows the condensation energies for even and odd N both for uniformly spaced and randomly spaced levels (discussions in [62, 80 and 73]).
Figure 8. Even and odd condensation energies are shown for uniform equally spaced level (dashed line) and ensemble-averaged energies for randomly spaced level (solid line). Vertical bars show fluctuations from [62] reported in [73].
Download figure:
Standard image High-resolution image4.6. Nano superconductivity in multiband systems
Earlier, in section 2, we have discussed multiband theories in the BCS and GL models. Particularly, two-band systems were analysed in some detail. From the material perspective Nb, Ta and V are the elemental metals which have two-band superconductivity [15]. Superconducting studies have been made in Nb-doped SrTiO3 in bulk [16]. After the discovery of two-band superconductivity in MgB2 [82] and Fe pnictides [83], important work continued to be done in multiband materials (see these two reviews [84, 85]).
In the area of nanosuperconductivity a number of studies have been reported. Quantum size effect (QSE) modulated superconductivity has been observed in nanograins of Pb on Si [86]. QSE has been studied in Pb, In and V [87–89], where nanosuperconductivity seems to obey the Anderson criterion. Authors of [90] have investigated size dependent Tc, coherence length, upper critical field 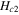 , and irreversible field
, and irreversible field 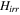 , in Nb. Reduction of the gap in ultra-thin films of Pb on Si by variation of thickness is reported in [91]. Magnetization in Pb nanoparticles has been studied in the range of 4–1000 nm [92]. The Meissner effect is clearly seen for particle sizes >30 nm, consistent with the Anderson criterion. Multilayer ultra-thin Pb films (5–15 monolayers) are the subject of a study of scanning tunnelling spectroscopy [93], where layer dependent superconducting gap and
, in Nb. Reduction of the gap in ultra-thin films of Pb on Si by variation of thickness is reported in [91]. Magnetization in Pb nanoparticles has been studied in the range of 4–1000 nm [92]. The Meissner effect is clearly seen for particle sizes >30 nm, consistent with the Anderson criterion. Multilayer ultra-thin Pb films (5–15 monolayers) are the subject of a study of scanning tunnelling spectroscopy [93], where layer dependent superconducting gap and 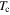 are reported. Superlattices of artificially engineered pnictide superconductors are fabricated for new interfacial phenomena and many device applications [94].
are reported. Superlattices of artificially engineered pnictide superconductors are fabricated for new interfacial phenomena and many device applications [94].
While experimental progress on multiband superconductivity is heading forward, there are some developments on the theoretical front. The possibility of superconductivity in doped SrTiO3 in films and interfaces is reported [95] by using a two-dimensional two-band model. Shape resonances and shell effects are investigated for multiband superconductors in thin film form [96]. In this work the one-band model of Blatt and Thompson [66] has been extended for two band superconductors relevant to MgB2 systems. From this work we show in figure 9 the calculated 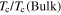 value as the film thickness varies. The implication of this calculation is that the pattern of the shape resonances is more regular as the offset
value as the film thickness varies. The implication of this calculation is that the pattern of the shape resonances is more regular as the offset  decreases. (Note, this offset is between the two σ and π bands.) In the one- band limit the shape resonances (blue colour) have larger amplitudes compared to the two-band case (black colour). Therefore, the size effect is suppressed by the multiband structure. For details see [96].
decreases. (Note, this offset is between the two σ and π bands.) In the one- band limit the shape resonances (blue colour) have larger amplitudes compared to the two-band case (black colour). Therefore, the size effect is suppressed by the multiband structure. For details see [96].
Figure 9. Tc/Tc(Bulk for MgB2 = 38 K) as a function of film thickness in nm for one-band (in blue colour) and two-band (black colour) limits. (See [96]).
Download figure:
Standard image High-resolution image4.7. Multiband nano superconductivity by BCS-Richardson model
In a long paper, Kruchinin and Nagao (KN) [97] considered a two-band superconductivity model (for MgB2) by extending Richardson's exact model. We describe this approach in some detail. They considered the two-band Hamiltonian as in the bulk for the nanograin.
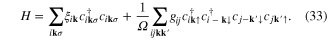
Unlike in the bulk, ks are now discrete state indices, js—band indices. 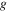 is the interaction matrix with attraction for the intra-band (
is the interaction matrix with attraction for the intra-band (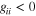 ) and repulsion (
) and repulsion (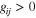 ) for the inter-band couplings. Since the states are discrete, the sums in the Hamiltonian are over the set
) for the inter-band couplings. Since the states are discrete, the sums in the Hamiltonian are over the set  of
of  states corresponding to band 1 with fixed width
states corresponding to band 1 with fixed width 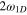 and the set
and the set 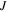 of
of  states for band 2, respectively. For simplicity one can assume Debye energies
states for band 2, respectively. For simplicity one can assume Debye energies  and
and 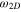 are the same and equal to
are the same and equal to 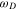 . Then
. Then 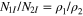 , where
, where 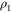 and
and  are density of states for respective bands. As in the Richardson's model the interaction energies are
are density of states for respective bands. As in the Richardson's model the interaction energies are 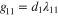 and
and 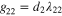 ,
, 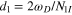 and
and 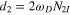 . The last two are the mean energy level spacings.
. The last two are the mean energy level spacings.  and
and 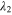 are dimensionless parameters for two sub-bands. The inter-band coupling is written as
are dimensionless parameters for two sub-bands. The inter-band coupling is written as  The ratio
The ratio 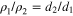 .
.
KN [98] employed the functional integral approach, commonly used in the problems of pairing correlations of a finite number of fermions [99, 100] With this technique the coupled gap equations at 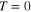 are obtained (for bulk) as
are obtained (for bulk) as 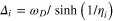 with
with 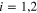 .
.
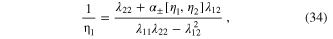
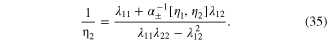
The phase of the gap is ![${{\alpha }_{\pm }}\left[ {{\eta }_{1}},{{\eta }_{2}} \right]=\pm {\rm sinh} \left( 1/{{\eta }_{2}} \right)/{\rm sinh} \left( 1/{{\eta }_{1}} \right)$](https://content.cld.iop.org/journals/2043-6262/6/1/013001/revision1/ansn505364ieqn252.gif) . Here there are two cases, (i) the phases can be same and (ii) the phases are opposite. When the inter-band coupling
. Here there are two cases, (i) the phases can be same and (ii) the phases are opposite. When the inter-band coupling 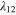 is large,
is large,  and for
and for 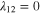 , bulk gaps are independent two gaps. These results we have obtained earlier by the GL method (section 2.2) for the bulk two-band superconductivity. KN calculates the condensate energy
, bulk gaps are independent two gaps. These results we have obtained earlier by the GL method (section 2.2) for the bulk two-band superconductivity. KN calculates the condensate energy  for the two-band nanosuperconductor. As conventionally defined it is the difference of ground state energies of normal and superconducting states including the interaction term. The final expression for the total condensation energy
for the two-band nanosuperconductor. As conventionally defined it is the difference of ground state energies of normal and superconducting states including the interaction term. The final expression for the total condensation energy 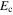 is given by
is given by
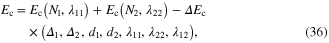
where the first two terms on the right hand side are condensation energy of two independent sub-systems and the last term is the contribution of inter-band contribution given by
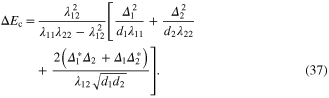
The quantity 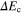 increases or decreases depending on the value of the phase difference.
increases or decreases depending on the value of the phase difference. 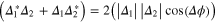 . If its value is
. If its value is  , it leads to an instability, whereas its value
, it leads to an instability, whereas its value 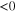 , makes
, makes 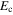 more stable. This we have discussed in section 2.1 under the multiband GL theory.
more stable. This we have discussed in section 2.1 under the multiband GL theory.
Among other things KN discusses critical level spacing, the parity gap, Kondo effect and application to quantum computing for this model.
4.8. Multiband nano superconductivity by extended GL model
This is a new paradigm of nanofilms involving multiband superconductors. Quantum confinement and fluctuations are important in quasi-2D systems. Therefore, it will be alluring to implement the extended GL method as worked out in detail for multiband bulk system in [39, 40]. Shanenko et al [100] have made a preliminary attempt in this realm. They have included terms of order 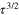 in the extended GL equation. Yet the validity of GL equations remains
in the extended GL equation. Yet the validity of GL equations remains 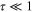 .
.
5. Epilogue
In this review we presented a bird's eye view of recent advances in novel superconductors. We gave a pedagogic brief history of superconducting phenomenon by presenting both theories and experiments. We begin with the one-band/gap superconductors. Phenomenological theory of GL and microscopic theory of BCS are outlined with an important landmark result. Gor'kov showed that the GL theory was derived from the BCS theory, particularly its correctness near Tc. There is a technical point that for the equivalence of both the theories, GL theory relies on the expansion of 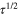 (
( ) in the lowest order.
) in the lowest order.
In view of possible occurrence of superconductivity in s-d band metals, multi-band generalization of GL and BCS was done by a number of workers. An important parameter appearing in these theories is the inter-band couplings, which show some interesting consequences such as, time reversed broken symmetry state, kink solutions and frustration. In the multiband case we showed the equivalence of GL and BCS models near the Tc. Going beyond the standard GL theory we made expansion of the order parameter to higher order in  . We showed some new results in the calculations of the order parameter compared to the BCS values.
. We showed some new results in the calculations of the order parameter compared to the BCS values.
After having stated these background materials we discussed superconductivity going from 'bulk to nano'. A criterion predicted by Anderson that superconductivity can survive in a small grain of material above a certain critical size is the main issue highlighted in the later part of the paper. In this context we discussed the BCS theory for finite size systems, what has been studied in great detail in nuclear physics for pairing of nucleons. An exactly solvable model due to Richardson for finite number of particles is discussed with many important results reviewed.
Physics being an experimental science, a large number and variety of experiments have been done recently on nanosuperconductivity. We have given an ample amount of information of this development. Arising out of this necessity of understanding the experiments, some highlights of theory are presented. With these prospects we are hopeful that there will be more investigations in this fast growing area.
Acknowledgments
MPD is grateful to Professor Nguyen Van Hieu for the kind invitation and warm hospitality that is immensely enjoyable coming to Ha Long City for the IWAMSN-2014.
Footnotes
- *
Keynote talk at the 7th International Workshop on Advanced Materials Science and Nanotechnology IWAMSN2014, 2-6 November, 2014, Ha Long, Vietnam