Abstract
Two-mode photon-added displaced squeezed states were previously introduced and their various interesting nonclassical as well as nonlocal properties were studied in great detail. In this paper we present experimental schemes for generating those states using optical devices such as nondegenerate parametric downconverters, displacers, beam-splitters and photo-detectors. The purpose is to see how close to the desired state the generated state can be and how high the success probability corresponding to a given fidelity is.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum optics distinguishes nonclassical from classical states and quantum information science distinguishes entangled from unentangled (or separable) states. Although developed almost independently and at different times (while the study of nonclassical states appeared just after the introduction of coherent states in the 1960s [1], the notion of entangled states had been encountered already in 1935 with respect to the completeness of quantum mechanics [2]), nonclassicality and entanglement are closely related. Most evident is the fact that no entanglement can be created at all by a beam-splitter from a classical source. In other words, for the output of a beam-splitter to be entangled the input should be nonclassical. Recently, a unified quantification of nonclassicality and entanglement has been put forward in [3] according to which the amount of nonclassicality of a (multimode) input field is exactly equal to the amount of (multipartite) entanglement of the output field. While nonclassical properties gave birth to new developments of the quantum coherence theory [4], entanglement has been recognized as a necessarily vital resource for quantum information processing and quantum computing, which are totally new ways of handling communication and computation [5].
There are many classes of nonclassical states: cat states [6], squeezed states [7], antibunched states [8], fan states [9], pair coherent states [10], trio coherent states [11], just to name a few. An interesting one called displaced squeezed state was introduced in [12]. Its extension to the two-mode case is of the form [13]

where 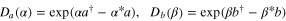 are the single-mode displacement operators (or displacers for short),
are the single-mode displacement operators (or displacers for short), 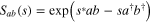 the two-mode squeezer,
the two-mode squeezer,  the state containing no photons in both modes
the state containing no photons in both modes  and
and 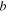 ,
,  the photon creation (annihilation) operator for mode
the photon creation (annihilation) operator for mode 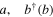 the same for mode
the same for mode 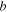 and
and 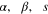 are complex in general. The authors of [13] also considered new states obtained by adding photons to either of the modes, focusing on the nonclassical behaviors of mean numbers, Mandel Q parameter, cross-correlation function and Wigner function. Such states have recently been generalized in [14] to the situation when photons are added to both modes, whose sum-squeezing, difference-squeezing, higher-order antibunching and entanglement were analyzed in detail. These generalized states called two-mode photon-added displaced squeezed states have the form
are complex in general. The authors of [13] also considered new states obtained by adding photons to either of the modes, focusing on the nonclassical behaviors of mean numbers, Mandel Q parameter, cross-correlation function and Wigner function. Such states have recently been generalized in [14] to the situation when photons are added to both modes, whose sum-squeezing, difference-squeezing, higher-order antibunching and entanglement were analyzed in detail. These generalized states called two-mode photon-added displaced squeezed states have the form
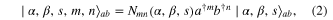
where

with
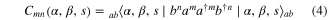
is the normalization coefficient. By virtue of the operatoric identities (α, β and s are assumed real for simplicity)

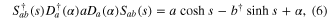
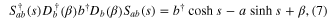
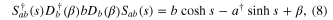
we can derive the expression of 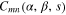 in the form which is useful for later numerical calculations as follows
in the form which is useful for later numerical calculations as follows

The study of photon addition has recently emerged as a topic of lively interest because this proves to be a plausible way to engineer on-demand quantum states (see, e.g. [15], and a nice review [16] with the references therein). In particular, adding photons always makes a classical state nonclassical. Also, many multimode photon-added states including the two-mode states (2) at the same time possess a certain amount of inter-mode entanglement that could be exploited to perform various useful global quantum tasks only by means of local operation combined with classical communication.
In this paper we are concerned with the techniques of how to add a desired number of photons to each of the two modes of the displaced squeezed state given by equation (1), i.e., how to generate the two-mode photon-added displaced squeezed states given by equation (2). Two different schemes for that purpose will be presented in the next section to see how close the generated state is to the target one and how the corresponding success probability could be, depending on the parameters involved. We shall briefly summarize and outline possible related problems in the final section.
2. The generation schemes
Although photon-added states were introduced many years ago [17], they had to wait until 2004 when a single-photon addition was actually realized for the first time in the laboratory [18]. Before going into any detail, it is worth at this point clarifying the real meaning of the terminologies 'photon-added' or 'adding photons' which may be misleading. A non-specialist would think that a photon-added state  with
with 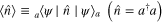 being the averaged photon number in the original state
being the averaged photon number in the original state  should be the state in which the averaged photon number becomes
should be the state in which the averaged photon number becomes  i.e., exactly one photon should be added. However, this is not true. In fact,
i.e., exactly one photon should be added. However, this is not true. In fact,  can be calculated to be
can be calculated to be 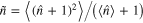 so that
so that  where
where 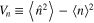 is the photon number variance, which vanishes only for a Fock state with a definite photon number. This implies
is the photon number variance, which vanishes only for a Fock state with a definite photon number. This implies  in general. In view of the above elucidation, we now correctly understand that 'adding
in general. In view of the above elucidation, we now correctly understand that 'adding  photons' to a state
photons' to a state  simply means
simply means  times of application of
times of application of 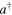 on that state. In this spirit and making use of the properties of currently available optical devices we shall in this section consider two schemes for generating the two-mode photon-added displaced squeezed states of the form (2). For implementing photon addition, the first scheme uses beam-splitters, while the second one employs nondegenerate parametric downconverters. Both schemes require photo-detectors which are assumed ideal photon-number-resolving for simplicity in theoretical calculations.
on that state. In this spirit and making use of the properties of currently available optical devices we shall in this section consider two schemes for generating the two-mode photon-added displaced squeezed states of the form (2). For implementing photon addition, the first scheme uses beam-splitters, while the second one employs nondegenerate parametric downconverters. Both schemes require photo-detectors which are assumed ideal photon-number-resolving for simplicity in theoretical calculations.
2.1. Photon addition by beam-splitters
Beam-splitter (BS), a device that transforms two input modes to two new output modes, is described by the unitary operator
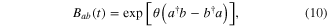
with  the transmittivity and
the transmittivity and  the reflectivity. Figure 1 sketches the arrangement of the devices necessary for the generation process. DC denotes a nondegenerate parametric downconverter described by the two-mode squeezer
the reflectivity. Figure 1 sketches the arrangement of the devices necessary for the generation process. DC denotes a nondegenerate parametric downconverter described by the two-mode squeezer  . In the downconversion process, a mother-photon from the beam that pumps a
. In the downconversion process, a mother-photon from the beam that pumps a  nonlinear medium gives birth to two daughter-photons belonging to two different modes labeled
nonlinear medium gives birth to two daughter-photons belonging to two different modes labeled  and
and  . Mode
. Mode 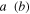 is then displaced by
is then displaced by  which can be implemented by means of a low-reflectivity (low-
which can be implemented by means of a low-reflectivity (low- ) and an intense coherent beam with amplitude
) and an intense coherent beam with amplitude 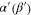 such that
such that 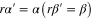 . As a result, the state
. As a result, the state  of the form (1) appears after such operations. To simulate the action of
of the form (1) appears after such operations. To simulate the action of 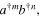 let mode
let mode  of state
of state 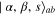 be an input to a beam-splitter (BS1) having transmittivity
be an input to a beam-splitter (BS1) having transmittivity  and, at the same time, mode
and, at the same time, mode 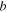 be an input to another beam-splitter (BS2) having the same transmittivity. As for the other input modes
be an input to another beam-splitter (BS2) having the same transmittivity. As for the other input modes  and
and  of BS1 and BS2, they are Fock states
of BS1 and BS2, they are Fock states 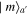 and
and 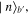 respectively. Behind the beam-splitters there are two photo-detectors, PD1 and PD2, to detect photons of outgoing modes
respectively. Behind the beam-splitters there are two photo-detectors, PD1 and PD2, to detect photons of outgoing modes 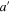 and
and 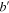 , respectively. We are interested in the case when neither detectors click, projecting the two modes
, respectively. We are interested in the case when neither detectors click, projecting the two modes  and
and  onto
onto
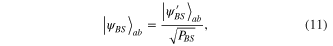
with
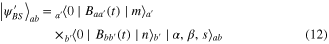
and

being the success probability (i.e., the probability that there are no clicks at all). Using the decomposition of the beam-splitter [19]
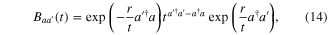
we have
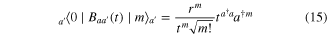
and

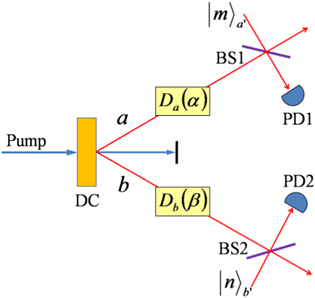
Figure 1. Schematic setup for generation of two-mode photon-added displaced squeezed states using beam-splitters for photon addition. A nondegenerate parametric downconverter DC followed by two displacers  and
and  are used to create states
are used to create states  in equation (1), while a Fock state
in equation (1), while a Fock state  , a beam-splitter BS1 (BS2) combined with a photo-detector PD1 (PD2) are used to add photons to mode
, a beam-splitter BS1 (BS2) combined with a photo-detector PD1 (PD2) are used to add photons to mode  . Success is heralded when no photons are registered by both the photo-detectors.
. Success is heralded when no photons are registered by both the photo-detectors.
Download figure:
Standard image High-resolution imageSubstituting equations (15) and (16) into equation (12) yields

Putting  and
and  in equation (17) in the form
in equation (17) in the form 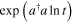 and
and  then using the equalities [20]
then using the equalities [20]
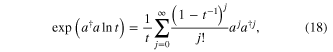

we can write 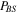 , equation (13), in the explicit form ready for numerical calculations as
, equation (13), in the explicit form ready for numerical calculations as

As for the fidelity 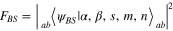 of the generated state (11) with respect to the target state (2), its explicit form reads
of the generated state (11) with respect to the target state (2), its explicit form reads

Precisely speaking, from equation (17), the net effect of the beam-splitters BS1 and BS2 in figure 1, conditioned on the outcome that no photons at all are detected by both detectors, is the action of  on
on  . So, a naïve inference would tell us that the desired addition of photons (i.e., the action of
. So, a naïve inference would tell us that the desired addition of photons (i.e., the action of  ) would be achieved if
) would be achieved if 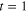 . However, such a mathematical 'result' cannot be accepted since it is unphysical: in fact, a beam-splitter with
. However, such a mathematical 'result' cannot be accepted since it is unphysical: in fact, a beam-splitter with  is tantamount to nothing and thus the state
is tantamount to nothing and thus the state  remains itself without any photons added. What can be expected is that the generated state would more resemble the intended one if
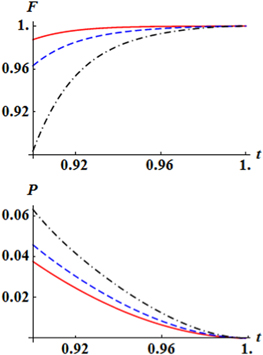
remains itself without any photons added. What can be expected is that the generated state would more resemble the intended one if  is getting closer to 1. To consolidate this we plot in figures 2 and 3 the fidelity (21) as a function of
is getting closer to 1. To consolidate this we plot in figures 2 and 3 the fidelity (21) as a function of 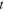 for several sets of the other parameters. As expected, the figures indicate that, though the fidelity can never be one, it always increases with
for several sets of the other parameters. As expected, the figures indicate that, though the fidelity can never be one, it always increases with  and asymptotically tends to 1 in the limit
and asymptotically tends to 1 in the limit 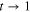 . The bad thing however is reduction of the corresponding success probability with increasing
. The bad thing however is reduction of the corresponding success probability with increasing  , as seen from their curves (see the bottom parts of figures 2 and 3), which also agrees with physical intuition. Namely, the greater
, as seen from their curves (see the bottom parts of figures 2 and 3), which also agrees with physical intuition. Namely, the greater 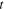 becomes, the easier the photons of mode
becomes, the easier the photons of mode 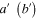 get through the beam-splitter BS1 (BS2) towards the detector PD1 (PD2) and, as a consequence, detection of no photons is less possible. Furthermore, as follows from figure 2, for given
get through the beam-splitter BS1 (BS2) towards the detector PD1 (PD2) and, as a consequence, detection of no photons is less possible. Furthermore, as follows from figure 2, for given  and
and  , both the fidelity and the corresponding generation probability decrease with increasing
, both the fidelity and the corresponding generation probability decrease with increasing  or/and
or/and  . Such a behavior of probability is due to the fact that the chance for a detector to click is proportional to the number of incoming photons. Practically, this implies that adding more photons is more challenging and, even when it succeeded, the price to pay is the reduction of fidelity. Finally, as seen from figure 3, for given
. Such a behavior of probability is due to the fact that the chance for a detector to click is proportional to the number of incoming photons. Practically, this implies that adding more photons is more challenging and, even when it succeeded, the price to pay is the reduction of fidelity. Finally, as seen from figure 3, for given  and
and  , the fidelity decreases but the corresponding success probability increases with increasing
, the fidelity decreases but the corresponding success probability increases with increasing  . Physically, these properties can be interpreted as follows. Here the state to which we add photons is
. Physically, these properties can be interpreted as follows. Here the state to which we add photons is  defined by equation (1). Its total averaged number of photons in both modes can be calculated to be
defined by equation (1). Its total averaged number of photons in both modes can be calculated to be  =
= 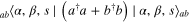 =
=  . Then, an increase in any of
. Then, an increase in any of  or/and
or/and  certainly raises
certainly raises  , thus triggering a decrease in the fidelity
, thus triggering a decrease in the fidelity 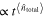 since
since  . As for the success probability behavior, when
. As for the success probability behavior, when  is high enough, a larger number of photons in mode
is high enough, a larger number of photons in mode  may cause fewer photons from both modes
may cause fewer photons from both modes  and
and  (
( and
and  ) to come into the photo-detector PD1 (PD2), thus increasing the possibility of no clicks. As a concrete situation, consider two states
) to come into the photo-detector PD1 (PD2), thus increasing the possibility of no clicks. As a concrete situation, consider two states  and
and  as inputs to BS1. The corresponding outputs will be
as inputs to BS1. The corresponding outputs will be  and
and  . For the first input state the probability of no clicks is
. For the first input state the probability of no clicks is  , while for the second input state the probability of no clicks is
, while for the second input state the probability of no clicks is  Clearly,
Clearly,  if
if 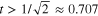 .
.
Figure 2. The fidelity  , equation (21), and the corresponding success probability
, equation (21), and the corresponding success probability 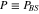 , equation (20), as functions of the beam-splitters' transmittivity
, equation (20), as functions of the beam-splitters' transmittivity  for
for 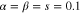 with
with 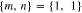 (red solid),
(red solid),  (blue dashed), and
(blue dashed), and 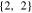 (black dash-dotted).
(black dash-dotted).
Download figure:
Standard image High-resolution imageFigure 3. The fidelity 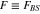 , equation (21), and the corresponding success probability
, equation (21), and the corresponding success probability 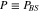 , equation (20), as functions of the beam-splitters' transmittivity
, equation (20), as functions of the beam-splitters' transmittivity  for
for  with
with 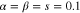 (red solid),
(red solid), 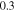 (blue dashed), and
(blue dashed), and 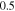 (black dash-dotted).
(black dash-dotted).
Download figure:
Standard image High-resolution image2.2. Photon addition by downconverters
The Fock states 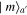 ,
, 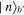 in the previous scheme are difficult to prepare and detections of no photons are also difficult to observe due to the always present vacuum noise. So, in this subsection we present an alternative way to add photons. Namely, nondegenerate parametric downconverters will be used instead of beam-splitters. The associated schematic setup is sketched in figure 4. Let the squeezing degree of both the downconverters DC2 and DC3 be
in the previous scheme are difficult to prepare and detections of no photons are also difficult to observe due to the always present vacuum noise. So, in this subsection we present an alternative way to add photons. Namely, nondegenerate parametric downconverters will be used instead of beam-splitters. The associated schematic setup is sketched in figure 4. Let the squeezing degree of both the downconverters DC2 and DC3 be  which is also assumed real for simplicity. The generation is regarded to be successful when at the same time PD1 registers
which is also assumed real for simplicity. The generation is regarded to be successful when at the same time PD1 registers  photons and PD2
photons and PD2  photons. If this event happens, it projects the states of modes
photons. If this event happens, it projects the states of modes  and
and 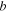 onto
onto

with

and
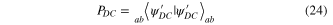
being the probability of successful generation. Using the decomposition of the two-mode squeezers [19]
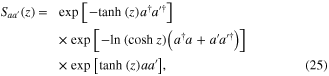
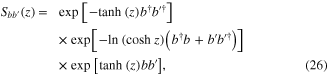
we can calculate the matrix elements in equation (23) and obtain

and
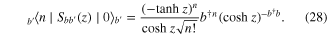
Figure 4. Schematic setup for generation of two-mode photon-added displaced squeezed states using downconverters for photon addition. A nondegenerate parametric downconverter DC1 combined with two displacers  and
and 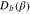 are used to create states
are used to create states  in equation (1), while a downconverter DC2 (DC3) combined with a photo-detector PD1 (PD2) are used to add photons to mode
in equation (1), while a downconverter DC2 (DC3) combined with a photo-detector PD1 (PD2) are used to add photons to mode 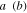 . Success is heralded when
. Success is heralded when  photons are registered by PD1 and
photons are registered by PD1 and  photons are registered by PD2, simultaneously.
photons are registered by PD2, simultaneously.
Download figure:
Standard image High-resolution imageSubstituting equations (27) and (28) into equation (23) yields
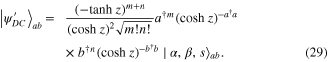
Using again the equalities (18) and (19) for 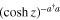 and
and  we can write
we can write 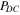 , equation (24), explicitly as
, equation (24), explicitly as
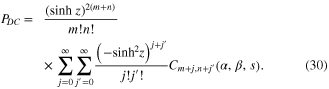
and the fidelity 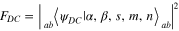 of the generated state (22) with respect to the target state (2) as
of the generated state (22) with respect to the target state (2) as

As seen from equation (29), the net effect of the downconverter DC2 (DC3) in figure 4, conditioned on the outcome that  photons are detected by the photo-detector PD1 (PD2), is the implementation of the action of
photons are detected by the photo-detector PD1 (PD2), is the implementation of the action of 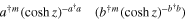 on mode
on mode  of the state
of the state  . So, the smaller the value of
. So, the smaller the value of  is the better
is the better  simulates
simulates 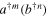 . This explains why in figures 5 and 6 the fidelity always decreases with increasing
. This explains why in figures 5 and 6 the fidelity always decreases with increasing  . For
. For  the fidelity is approaching but never reaches
the fidelity is approaching but never reaches  because when
because when 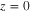 nothing will occur. An increase in the fidelity when
nothing will occur. An increase in the fidelity when  is decreasing is, however, accompanied with a decrease in the corresponding success probability, as shown by the bottom parts of figures 5 and 6. This is due to the properties of two-mode squeezers which are reflected by equations (27) and (28). Furthermore, figure 5 shows that, for given
is decreasing is, however, accompanied with a decrease in the corresponding success probability, as shown by the bottom parts of figures 5 and 6. This is due to the properties of two-mode squeezers which are reflected by equations (27) and (28). Furthermore, figure 5 shows that, for given 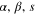 and
and  , both the fidelity and generation probability decrease with increasing
, both the fidelity and generation probability decrease with increasing  or/and
or/and  . This agrees with the case of using beam-splitters in the previous subsection that adding more photons is both worse in quality and more difficult in realization. Finally, similar to the beam-splitter-based scheme, the fidelity decreases but the corresponding success probability increases with increasing
. This agrees with the case of using beam-splitters in the previous subsection that adding more photons is both worse in quality and more difficult in realization. Finally, similar to the beam-splitter-based scheme, the fidelity decreases but the corresponding success probability increases with increasing  for given
for given  and
and  as observed from figure 6.
as observed from figure 6.
Figure 5. The fidelity 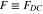 , equation (31), and the corresponding success probability
, equation (31), and the corresponding success probability 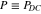 , equation (30), as functions of squeezing degree
, equation (30), as functions of squeezing degree  of the two two-mode squeezers for
of the two two-mode squeezers for 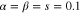 with
with 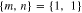 (red solid),
(red solid),  (blue dashed), and
(blue dashed), and  (black dash-dotted).
(black dash-dotted).
Download figure:
Standard image High-resolution imageFigure 6. The fidelity  , equation (31), and the corresponding success probability
, equation (31), and the corresponding success probability  , equation (30), as functions of squeezing degree
, equation (30), as functions of squeezing degree  of the two two-mode squeezers for
of the two two-mode squeezers for 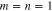 with
with  (red solid),
(red solid), 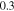 (blue dashed), and
(blue dashed), and  (black dash-dotted).
(black dash-dotted).
Download figure:
Standard image High-resolution image3. Conclusion
In summary, we have presented possible experimental setups for generation of the two-mode photon-added displaced squeezed state whose properties were investigated in detail previously. The focus is on the techniques of how to add arbitrary numbers of photons to each of the two modes of the displaced squeezed states. We considered two schemes for photon addition: one uses high-transmittivity (high- ) beam-splitters and the other uses small-squeezing degree (small-
) beam-splitters and the other uses small-squeezing degree (small- ) nondegenerate parametric downconverters. For each scheme the fidelity of the generated state with respect to the target one as well as the corresponding success probability were derived analytically and displayed graphically in dependence on all the parameters involved. We show that, though perfect generation (i.e., unit fidelity with unit success probability) is impossible, the fidelity is approaching
) nondegenerate parametric downconverters. For each scheme the fidelity of the generated state with respect to the target one as well as the corresponding success probability were derived analytically and displayed graphically in dependence on all the parameters involved. We show that, though perfect generation (i.e., unit fidelity with unit success probability) is impossible, the fidelity is approaching  for
for  tending to
tending to  or
or  tending to
tending to  , at the cost of vanishing success probability. As a consequence, a tradeoff should be made towards achieving sufficiently high fidelity accompanied with reasonably not too low success probability. All the devices used are currently available except the ideal number-resolving photo-detectors. Use of real nonideal photo-detectors with certain efficiency results in mixed states with much lower fidelity. Therefore, additional methods to purify the generated states as well as to improve their fidelity are welcome before one can apply them in quantum information processing. Besides, people are now also interested in photon subtraction [21] which is also a very useful tool to engineer quantum states. Hence, studying two-mode photon-subtracted displaced squeezed states seems to be a good topic for this work to follow. This would also provide a chance to closely compare differences and similarities between adding photons to and subtracting photons from the two-mode displaced squeezed states.
, at the cost of vanishing success probability. As a consequence, a tradeoff should be made towards achieving sufficiently high fidelity accompanied with reasonably not too low success probability. All the devices used are currently available except the ideal number-resolving photo-detectors. Use of real nonideal photo-detectors with certain efficiency results in mixed states with much lower fidelity. Therefore, additional methods to purify the generated states as well as to improve their fidelity are welcome before one can apply them in quantum information processing. Besides, people are now also interested in photon subtraction [21] which is also a very useful tool to engineer quantum states. Hence, studying two-mode photon-subtracted displaced squeezed states seems to be a good topic for this work to follow. This would also provide a chance to closely compare differences and similarities between adding photons to and subtracting photons from the two-mode displaced squeezed states.
Acknowledgements
T X H N is grateful to Danang University's College of Education, Hue University's College of Education and Hue Center for Theoretical and Computational Physics for encouraging her in pursuing research work.