Abstract
In this work we study the enhancement of the electromagnetic field in the free space surrounding metallic nanoparticles due to the effect of their localized plasmon resonance. We start from a review of the known results in the case of a simple metallic spherical nanoparticle and then extend these results to the general case of any network of many identical spherical metallic nanoparticles. For illustration, some typical lattices of identical spherical metallic nanoparticles will be investigated. Analytical expressions and algebraic equations determining the electromagnetic field in the free space surrounding these typical networks will be derived.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the appearance of the celebrated article of Fujishima and Honda [1] on pure water splitting in a photoelectrochemical cell with a titania photoanode, many research works on utilizing the visible light responsive titania-based nanostructures for the fabrication of the photoanodes of the photocatalytic, photoelectrochemical and photovoltaic cells have been performed (see, for example, a recent review [2] and references therein). Besides anion- and cation-doping titania to create the materials with energy band gaps narrower than that of pure titania, as well as sensitizing titania by dyes or quantum dots, it was also proposed to enhance the photocatalytic activity of titania under the action of visible light by loading nanoparticles of noble metals Au and Ag on pure titania and profiting from the localized plasmon resonance (LPR) effect of these metallic nanoparticles [3–24]. In this work we present the basics of the theory of the light enhancement due to the LPR effect in the metallic nanoparticles.
We start the presentation by considering the enhancement of the electrical field of the electromagnetic radiation nearby a metallic spherical nanoparticle due to the LPR effect. The related key formulae were known in the literature [25, 26]. Then we shall establish the general theory of the enhancement of the electrical field in the electromagnetic radiation near some arbitrary network of identical metallic spherical nanoparticles due to the LPR effect in these nanoparticles. For illustration and also for future applications, the enhanced electrical field of the electromagnetic radiation due to the LPR effect on some particular systems of identical metallic spherical nanoparticles will be investigated.
For the description of the electromagnetic field in vacuum or in a homogeneous medium outside the sources, it is convenient to work in a special Lorentz gauge with the vanishing scalar potential of the electromagnetic field. Then the physical state of the electromagnetic field is completely determined by its vector potential
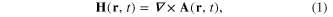
and the electrical field  is derived from the solution of the Maxwell equation
is derived from the solution of the Maxwell equation
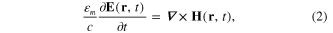
where  m
is the dielectrical constant of the medium. In the case of a monochromatic electromagnetic field with the angular frequency ω, equation (2) becomes
m
is the dielectrical constant of the medium. In the case of a monochromatic electromagnetic field with the angular frequency ω, equation (2) becomes
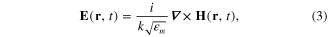
where  [26]. Formulae (1) and (3) will be used in the sequel.
[26]. Formulae (1) and (3) will be used in the sequel.
2. Single metallic spherical nanoparticle
Suppose that there exists a metallic spherical nanoparticle with radius ρ, and denote by 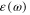 the effective dielectric constant or electric permittivity of the metallic material with respect to the electrical field in the monochromatic electromagnetic radiation with the angular frequency ω, by
the effective dielectric constant or electric permittivity of the metallic material with respect to the electrical field in the monochromatic electromagnetic radiation with the angular frequency ω, by  m
that of the dielectric medium surrounding the metallic nanoparticle. It was known that the electrical field
m
that of the dielectric medium surrounding the metallic nanoparticle. It was known that the electrical field

of the linearly polarized monochromatic incident light induces following electrical dipole moment 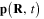 inside the metallic spherical nanoparticle with the center located at some point R in the space [25]:
inside the metallic spherical nanoparticle with the center located at some point R in the space [25]:
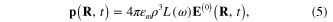
where

The induced electrical dipole moment located at some point R emits into the surrounding space the electromagnetic radiation which will be called the induced electromagnetic field described by the vector potential 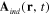 or by a set of the induced electrical field
or by a set of the induced electrical field 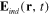 and induced magnetic field
and induced magnetic field 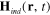 . It was shown (reference [26]) that near the location of the induced dipole moment (5) the vector potential
. It was shown (reference [26]) that near the location of the induced dipole moment (5) the vector potential 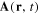 has the form
has the form

It follows that the induced electrical field  equals
equals
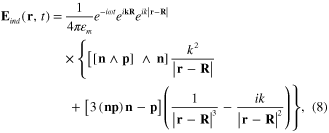
where
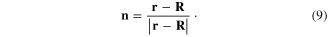
At a point r very near to the metallic spherical nanoparticle, 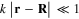 , formula (7) has following approximate form
, formula (7) has following approximate form

In terms of the components 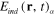 of
of  and the components pα
of the induced electrical dipole moment p, formula (8) can be rewritten in the form
and the components pα
of the induced electrical dipole moment p, formula (8) can be rewritten in the form

where
Formulae (5), (6) and (8) show that the enhancement effect due to the presence of a metallic spherical nanoparticle with the diameter ρ depends on the value of the function L(ω) expressed in terms of the electric permittivity  (ω) of the metal at the photon energy
(ω) of the metal at the photon energy 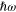 . From the experimental data on
. From the experimental data on  (ω) of gold (see appendix) there follow the values of the real and imaginary parts of L(ω) presented in figure 1.
(ω) of gold (see appendix) there follow the values of the real and imaginary parts of L(ω) presented in figure 1.
Figure 1. Real (a) and imaginary (b) parts of L(ω).
Download figure:
Standard image High-resolution imageFor the evident expression of the relationship between the induced electric field Eind(r, t) at a point r outside the metallic spherical nanoparticle and the electric field E(0)(R,t) of the incident light at the point R coinciding with the center of the metallic spherical nanoparticle (when it is absent) we chose this center to be the origin of the coordinate system (R = 0) and the vector r to be parallel to E(0). Then from formulae (5), (6) and (8) we have
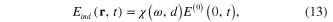
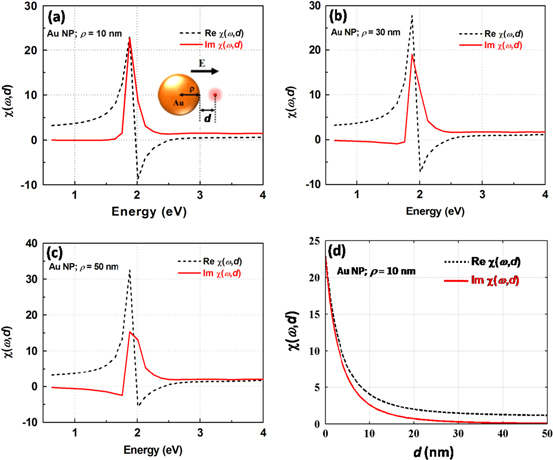
where d = r − ρ. The values of real and imaginary parts of χ(ω,d) versus ω at different distances d for the metallic spherical nanoparticle are presented in figures 2(a)–(d), the observation point r and the direction of the electrical field E(0) are shown in the inset of figure 2(a).
Figure 2. Real and imaginary parts of χ(ω,d) at d = 0 versus energy 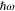 for the spheres with different radii. (a) ρ = 10 nm, (b) ρ = 30 nm, (c) ρ = 50 nm and (d) their maxima versus distance d for the sphere with ρ = 10 nm.
for the spheres with different radii. (a) ρ = 10 nm, (b) ρ = 30 nm, (c) ρ = 50 nm and (d) their maxima versus distance d for the sphere with ρ = 10 nm.
Download figure:
Standard image High-resolution image3. Network of identical metallic spherical nanoparticles
The main part of the present work is the establishment of the system of equations determining the enhanced electrical field in the spatial region surrounding a network of identical metallic spherical nanoparticles when this network is illuminated by a linearly polarized monochromatic light beam. Being induced by the electrical field of the incident light, each metallic nanoparticle as a dipole moment itself emits the electromagnetic radiation into the surrounding space. Therefore, the total electrical field at any point r nearby but outside the metallic nanoparticles must be the superposition of the electrical fields  of the electromagnetic radiations emitted by the induced electrical dipole moments
of the electromagnetic radiations emitted by the induced electrical dipole moments  and that of the incident light beam:
and that of the incident light beam:
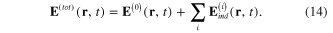
However, the total electrical field 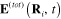 acting on the induced electrical dipole moment
acting on the induced electrical dipole moment  located at the point
located at the point 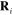 is the superposition of the electrical field
is the superposition of the electrical field 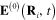 of the incident light and the electrical fields
of the incident light and the electrical fields  in the electromagnetic radiations emitted by other induced electrical dipole moments
in the electromagnetic radiations emitted by other induced electrical dipole moments 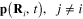 :
:
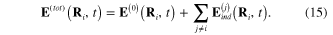
Because this total electrical field induces the electrical dipole moment 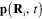 , according to formula (5) we have
, according to formula (5) we have
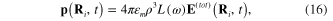
Let us write the induced dipole moment (16) in the form
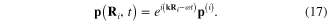
From the expression (8) it follows that
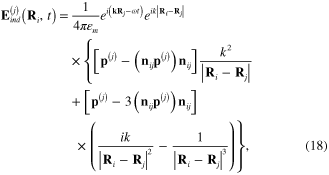
where
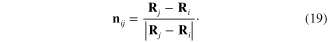
In terms of the components  of the electrical field
of the electrical field  and the components
and the components  of the induced electrical dipole moment
of the induced electrical dipole moment  , formula (18) can be rewritten as follows:
, formula (18) can be rewritten as follows:
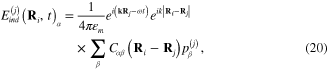
where
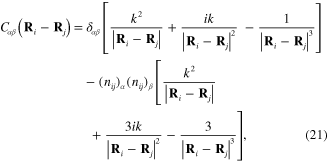
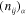 being components of the vector
being components of the vector  .
.
By using equations (15), (16) and (18) as well as expressions (4) and (17), it is straightforward to derive the system of algebraic equations for determining the induced electrical dipole moments  of the metallic spherical nanoparticles in the network:
of the metallic spherical nanoparticles in the network:

In terms of the components 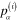 of the induced electrical dipole moments
of the induced electrical dipole moments 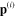 and the components
and the components 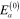 of the electric field
of the electric field 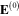 in the incident radiation, system of equation (22) becomes
in the incident radiation, system of equation (22) becomes
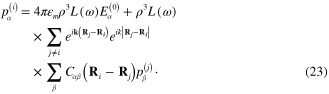
By solving the system of equations (22) or (23), we find the functions  determining the components of the induced electrical dipole moments of all metallic spherical nanoparticles in the network.
determining the components of the induced electrical dipole moments of all metallic spherical nanoparticles in the network.
Formula (8) or (11) determines the electrical field of the electromagnetic radiation emitted by the electrical dipole moment

From these formulae it is easy to derive the expression of the total electrical field (14)

where
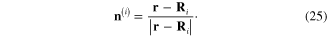
In terms of the components  and
and  of the electrical fields
of the electrical fields 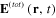 and
and 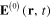 as well as the components
as well as the components 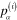 of the induced electrical dipole moments
of the induced electrical dipole moments  , formula (24) becomes
, formula (24) becomes
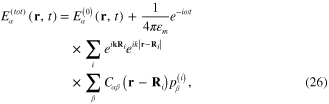
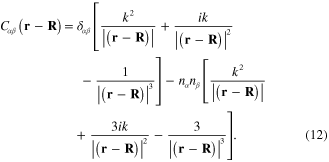
where 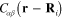 is determined by following expression similarly to formula (12)
is determined by following expression similarly to formula (12)

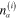 being the components of vector
being the components of vector 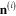 defined by formula (25).
defined by formula (25).
Finally we remark that the Hamiltonian of the interaction between the total electromagnetic field induced by all metallic nanoparticles in the network with the individual electrons and holes in the whole system explicitly contains the vector potential 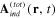 of the total electromagnetic field emitted by all electrical dipole moments
of the total electromagnetic field emitted by all electrical dipole moments 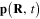 induced on all nanoparticles
induced on all nanoparticles
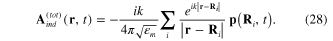
4. Simple examples
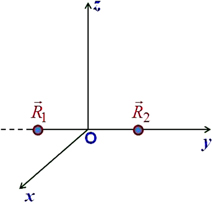
Consider first the simplest case of a system of two identical metallic spherical nanoparticles with the radius ρ located at the distance l ( ). This system is called a dimer. We choose to work in such a Cartesian coordinate system that the centers
). This system is called a dimer. We choose to work in such a Cartesian coordinate system that the centers 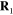 and
and  of two metallic spherical nanoparticles are located at two points with the coordinates
of two metallic spherical nanoparticles are located at two points with the coordinates 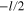 and
and 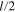 , respectively, in the axis Oy (figure 3), and consider the behaviour of the dimer in the presence of a monochromatic incident electromagnetic field with the wave vector k paralled to the axis Oz: k//Oz.
, respectively, in the axis Oy (figure 3), and consider the behaviour of the dimer in the presence of a monochromatic incident electromagnetic field with the wave vector k paralled to the axis Oz: k//Oz.
Figure 3. Two metallic spherical nanoparticles.
Download figure:
Standard image High-resolution imageIt is straightforward to derive the system of equation (22) for two induced electrical dipole moments  and
and 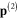 of two metallic spherical nanoparticles. If the incident electromagnetic wave is linearly polarized along the axis Oy, then we have following system of equations
of two metallic spherical nanoparticles. If the incident electromagnetic wave is linearly polarized along the axis Oy, then we have following system of equations
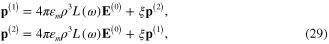
where
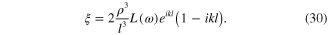
Its solution is
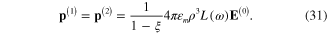
In comparison with formula (5) for the induced electrical dipole moment of a single metallic spherical nanoparticle there arises the factor 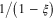 . Similarly, if the incident electromagnetic wave is linearly polarized along the axis Ox, then the induced electrical dipole moments
. Similarly, if the incident electromagnetic wave is linearly polarized along the axis Ox, then the induced electrical dipole moments  and
and 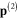 of two metallic spherical nanoparticles must satisfy following system of equations
of two metallic spherical nanoparticles must satisfy following system of equations
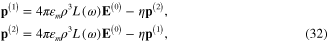
where

Its solution is

In comparison with formula (5) now there arises the factor  .
.
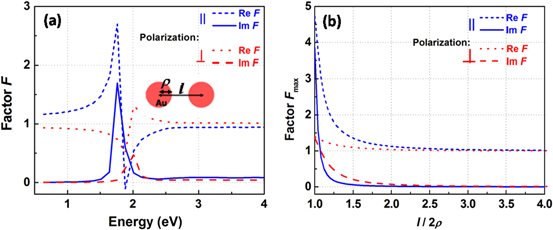
The enhancement of the electrical dipole moment of each spherical nanoparticle due to the mutual influence of the other is characterized by the so-called enhancement factor F which is equal to 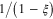 in the case when their polarization direction (that of the electrical field E(0)) is parallel to the Oy axis and is equal to
in the case when their polarization direction (that of the electrical field E(0)) is parallel to the Oy axis and is equal to 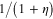 in the case of polarization perpendicular to the Oy axis. The values of the complex values of the enhancement factor F for a dimer consisting of two identical metallic nanospheres with the radius ρ = 10 nm and placed at the distance l = 25 nm of their centers have been calculated on the basis of formulae (30) and (33). They depend on the photon energy
in the case of polarization perpendicular to the Oy axis. The values of the complex values of the enhancement factor F for a dimer consisting of two identical metallic nanospheres with the radius ρ = 10 nm and placed at the distance l = 25 nm of their centers have been calculated on the basis of formulae (30) and (33). They depend on the photon energy 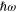 and are plotted in figure 4(a) for both configurations of the arrangement of the polarization of the electrical field and the Oy axis. The picture of the dimer is presented in the inset of this figure. The dependence of the maximum values of the real and imaginary parts of the enhancement factor F for both configurations on the distance between two centers of two metallic spherical nanoparticles is presented in figure 4(b).
and are plotted in figure 4(a) for both configurations of the arrangement of the polarization of the electrical field and the Oy axis. The picture of the dimer is presented in the inset of this figure. The dependence of the maximum values of the real and imaginary parts of the enhancement factor F for both configurations on the distance between two centers of two metallic spherical nanoparticles is presented in figure 4(b).
Figure 4. (a) Photon energy dependence of the real (black) and imaginary (red) part of the enhancement factor F of the dimer with ρ = 10 nm, l = 25 nm for both configurations. (b) Dependence of the real (black) and imaginary (red) part of the enhancement factor F of the dimer with ρ = 10 nm on the ratio l/2ρ.
Download figure:
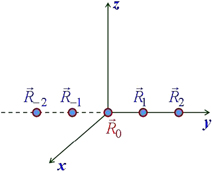
Standard image High-resolution imageThe second simple example of a network of identical metallic sphere nanoparticles is a linear chain of equidistant ones with the centers located at the points 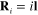 , i being integers and l being some vector (figure 5). The center R0 of one spherical nanoparticle is the origin of the coordinate system. Suppose that the wave vector k is perpendicular to the direction of the chain: kl = 0. In the case of the linearly polarized incident electromagnetic wave with the electrical field
, i being integers and l being some vector (figure 5). The center R0 of one spherical nanoparticle is the origin of the coordinate system. Suppose that the wave vector k is perpendicular to the direction of the chain: kl = 0. In the case of the linearly polarized incident electromagnetic wave with the electrical field 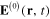 parallel to the direction of the chain,
parallel to the direction of the chain,  , the values
, the values  of the induced electrical dipole moments are determined by following system of equations
of the induced electrical dipole moments are determined by following system of equations

Figure 5. Linear chain of equidistant metallic spherical nanoparticles.
Download figure:
Standard image High-resolution imageFor the infinite linear chain, due to the translational invariance of this chain, the solution of equation (35) is
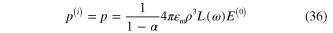
with

Similarly, in the case of the linearly polarized incident electromagnetic wave with the electrical field  perpendicular to the direction of the chain,
perpendicular to the direction of the chain, 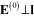 , we have following system of equations
, we have following system of equations

For the infinite linear chain its solution is

with

According to formulae (36) and (39) the enhancement factor F is equal to  in the case of the electrical field
in the case of the electrical field 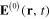 parallel to the direction of the chain and it is equal to
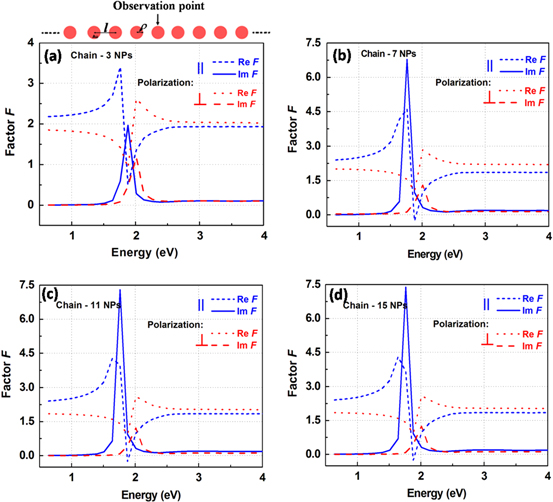
parallel to the direction of the chain and it is equal to 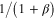 in the case of the electrical field perpendicular to the direction of the chain. The numerical calculations have been done for the chain consisting of 3, 7, 11 and 15 identical metallic spherical nanoparticles with the radius ρ = 10 nm and with the distance of two nearest ones l = 25 nm. The photon energy
in the case of the electrical field perpendicular to the direction of the chain. The numerical calculations have been done for the chain consisting of 3, 7, 11 and 15 identical metallic spherical nanoparticles with the radius ρ = 10 nm and with the distance of two nearest ones l = 25 nm. The photon energy 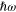 dependent real (black) and imaginary (red) parts of the enhancement factor F for both polarization configurations are plotted in figure 6.
dependent real (black) and imaginary (red) parts of the enhancement factor F for both polarization configurations are plotted in figure 6.
Figure 6. Photon energy dependence of the real (black) and imaginary (red) parts of the enhancement factor F of a chain consisting of (a) 3; (b) 7, (c) 11 and (d) 15 identical metallic spherical nanoparticles of the dimer with ρ = 10 nm, l = 25 nm for both configurations.
Download figure:
Standard image High-resolution imageThe third network, which would be more often used, is that of a two-dimensional square lattice of identical metallic spherical nanoparticles with their centers located at the points  , i and j being integers, ex
and ey
being the unit vectors along the coordinate axes Ox and Oy, respectively, l being the nearest distance between two spherical nanoparticles (figure 7). We write the dipole moment induced on the spherical metallic nanoparticle with the center located at the point
, i and j being integers, ex
and ey
being the unit vectors along the coordinate axes Ox and Oy, respectively, l being the nearest distance between two spherical nanoparticles (figure 7). We write the dipole moment induced on the spherical metallic nanoparticle with the center located at the point 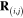 in the form similarly to expression (17):
in the form similarly to expression (17):
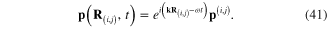
Figure 7. The network of a two-dimensional square lattice of identical metallic spherical nanoparticles with their centers located at the points R(i,j).
Download figure:
Standard image High-resolution imageFor definiteness we choose the center  of one spherical nanoparticle to be the origin of the coordinate system. Suppose that the wave vector k of the incident light is perpendicular to the plane of the network:
of one spherical nanoparticle to be the origin of the coordinate system. Suppose that the wave vector k of the incident light is perpendicular to the plane of the network: 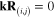 , and consider the case when the incident electromagnetic wave is linearly polarized and has the electrical field
, and consider the case when the incident electromagnetic wave is linearly polarized and has the electrical field  parallel to the direction of the axis Ox. It is straightforward to derive following system of algebraic equations determining the induced electrical dipole moments
parallel to the direction of the axis Ox. It is straightforward to derive following system of algebraic equations determining the induced electrical dipole moments 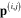 :
:
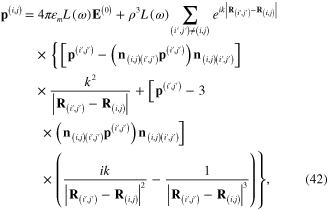
where

Due to the translational invariance of the infinite square lattice, the solution of the system of equation (42) for the network of infinite square lattice of identical metallic spherical nanoparticles becomes
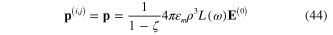
with

The first term in the rhs of equation (45) is expression (37) of the constant α in formula (36) for the induced electrical dipole moment in the infinite linear chain of identical metallic spherical equidistant nanoparticles located in the real axis Ox, while remaining terms are the contributions of all other linear chains different from that in the real axis Ox.
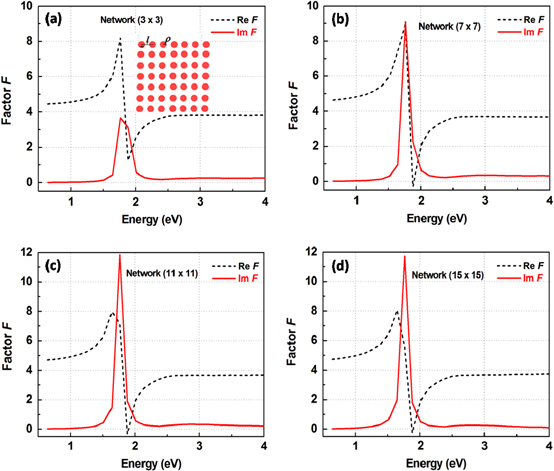
The photon energy 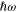 dependent values of the real (black) and imaginary (red) parts of the enhancement factor F (equal to
dependent values of the real (black) and imaginary (red) parts of the enhancement factor F (equal to  ) of the square networks of
) of the square networks of  metallic spherical nanoparticles with n = 3, 7, 11 and 15 are presented in figure 8.
metallic spherical nanoparticles with n = 3, 7, 11 and 15 are presented in figure 8.
Figure 8. Photon energy dependence of the complex enhancement factor F of the square networks of (a) 3 × 3, (b) 7 × 7, (c) 11 × 11 and (d) 15 × 15 metallic spherical nanoparticles with ρ = 10 nm and distance of two nearest ones l = 25 nm.
Download figure:
Standard image High-resolution imageOther more complicated networks of identical metallic spherical nanoparticles can also be considered in a similar manner. From the expressions of the induced electrical dipole moments p(i) of the metallic spherical nanoparticles it is now straightforward to calculate the total electrical field 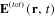 of the resulting electromagnetic radiation in the space by using formulae (24)–(27).
of the resulting electromagnetic radiation in the space by using formulae (24)–(27).
5. Conclusion and discussion
In this work, on the basis of formula (5) for the electrical dipole moment 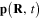 induced on a metallic spherical nanoparticle with the radius ρ and the center located at the point R by the interaction of the electrical field
induced on a metallic spherical nanoparticle with the radius ρ and the center located at the point R by the interaction of the electrical field  of the form (4) with the conduction electrons inside this nanoparticle as well as of formula (8) for the electrical field
of the form (4) with the conduction electrons inside this nanoparticle as well as of formula (8) for the electrical field 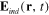 in the electromagnetic radiation emitted by the electrical dipole moment
in the electromagnetic radiation emitted by the electrical dipole moment 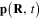 , we have investigated any network of nearby located identical metallic spherical nanoparticles and derived the systems of equations (22) and (23) determining their induced electrical dipole moments, taking into account the mutual electromagnetic interaction between these metallic nanoparticles. From this result there follow expressions (24)–(27) of the total electrical field
, we have investigated any network of nearby located identical metallic spherical nanoparticles and derived the systems of equations (22) and (23) determining their induced electrical dipole moments, taking into account the mutual electromagnetic interaction between these metallic nanoparticles. From this result there follow expressions (24)–(27) of the total electrical field 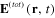 which was enhanced in comparison with the electrical field
which was enhanced in comparison with the electrical field 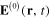 in the incident electromagnetic radiation due to the presence of the network of metallic spherical nanoparticles. The magnitude of the enhancement significantly depends on two quantities: the ratio ρ/l of the radius ρ of each nanoparticle to the distance l between two nearest nanoparticles in the network, and the parameter L(ω) defined by formula (6).
in the incident electromagnetic radiation due to the presence of the network of metallic spherical nanoparticles. The magnitude of the enhancement significantly depends on two quantities: the ratio ρ/l of the radius ρ of each nanoparticle to the distance l between two nearest nanoparticles in the network, and the parameter L(ω) defined by formula (6).
Denote by ωp
the plasma frequency of the free electron gas in the metallic material of the nanoparticles and by γ the characteristic collision frequency in this electron gas. At the frequency angular ω near the plasmon resonance, the electric permitivity  (ω) of the metallic material has the approximate form [25]
(ω) of the metallic material has the approximate form [25]

(usually 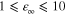 ). From definition (6) it follows that
). From definition (6) it follows that

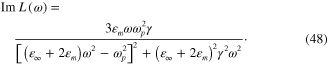
At the localized plasma resonance of a metallic spherical nanoparticle  with
with
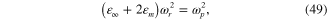
we have
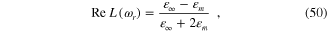
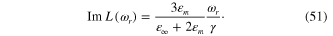
Since  , the enhancement effect is significant at the localized plasmon resonance frequency
, the enhancement effect is significant at the localized plasmon resonance frequency  .
.
Acknowledgments
The authors would like to express their gratitude to Academician Nguyen Van Hieu for suggesting this problem and for his encouragement, and to Vietnam Academy of Science and Technology and Institute of Materials Science for the support.
Appendix
The optical constants n (index of refraction) and k (the absorption coefficient) of gold were experimentally measured by Johnson and Christy [27]. From the values of the photon energy dependent physical parameters n(ω) and k(ω) we can obtain immediately the real and imaginary parts 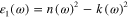 and
and 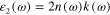 of the electric permittivity of gold and subsequently to calculate the real and imaginary parts L1(ω) and L2(ω) of the function L(ω) defined by formula (6) with the value
of the electric permittivity of gold and subsequently to calculate the real and imaginary parts L1(ω) and L2(ω) of the function L(ω) defined by formula (6) with the value  m
= 6.45 of the dielectric constant of titania. The results are presented in table 1.
m
= 6.45 of the dielectric constant of titania. The results are presented in table 1.
Table 1. Photon energy dependent values of the permittivity of gold and of L(ω).
| Energy (eV) | Wavelength (nm) |
 1 1
|
 2 2
|
L1 | L2 |
|---|---|---|---|---|---|
| 0.64 | 1937.50 | −189.042 | 25.355 | 1.108 | 0.015 |
| 0.77 | 1610.39 | −125.351 | 12.555 | 1.170 | 0.019 |
| 0.89 | 1393.26 | −90.426 | 8.186 | 1.247 | 0.026 |
| 1.02 | 1215.69 | −66.129 | 5.702 | 1.359 | 0.038 |
| 1.14 | 1087.72 | −51.050 | 3.861 | 1.502 | 0.051 |
| 1.26 | 984.13 | −40.274 | 2.794 | 1.700 | 0.071 |
| 1.39 | 892.09 | −32.041 | 1.925 | 2.001 | 0.101 |
| 1.51 | 821.19 | −25.811 | 1.627 | 2.476 | 0.186 |
| 1.64 | 756.10 | −20.610 | 1.272 | 3.445 | 0.403 |
| 1.76 | 704.55 | −16.818 | 1.067 | 5.603 | 1.254 |
| 1.88 | 659.57 | −13.648 | 1.035 | 9.865 | 12.317 |
| 2.01 | 616.92 | −10.662 | 1.374 | −5.276 | 3.848 |
| 2.13 | 582.16 | −8.113 | 1.661 | −2.607 | 1.250 |
| 2.26 | 548.67 | −5.842 | 2.111 | −1.526 | 0.752 |
| 2.38 | 521.01 | −3.946 | 2.580 | −0.995 | 0.575 |
| 2.50 | 496.00 | −2.278 | 3.813 | −0.614 | 0.579 |
| 2.63 | 471.48 | −1.703 | 4.844 | −0.456 | 0.630 |
| 2.75 | 450.91 | −1.759 | 5.283 | −0.418 | 0.672 |
| 2.88 | 430.56 | −1.692 | 5.649 | −0.377 | 0.694 |
| 3.00 | 413.33 | −1.702 | 5.717 | −0.371 | 0.700 |
| 3.12 | 397.44 | −1.649 | 5.739 | −0.365 | 0.696 |
| 3.25 | 381.54 | −1.605 | 5.644 | −0.371 | 0.685 |
| 3.37 | 367.95 | −1.401 | 5.609 | −0.359 | 0.663 |
| 3.50 | 354.29 | −1.232 | 5.598 | −0.348 | 0.647 |
| 3.62 | 342.54 | −1.310 | 5.538 | −0.359 | 0.649 |
| 3.74 | 331.55 | −1.355 | 5.574 | −0.359 | 0.656 |
| 3.87 | 320.41 | −1.231 | 5.846 | −0.326 | 0.664 |
| 3.99 | 310.78 | −1.243 | 5.793 | −0.331 | 0.661 |