Abstract
The transfer of quantum states along spin chains with the XY Heisenberg exchange interaction between nearest-neighbour spins and without decoherence was studied. It was shown that there exists a wide class of engineered mirror-symmetric N-spin-chains that allow the perfect quantum state transfer from one end of each chain to the other. The sets of values of physical parameters of these N-spin-chains were established.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
For the application to quantum information processing technology, quantum state transfer (QST) between two directly interacting qubits, as well as between two distant ones interacting through the intermediary of different quantum systems, was widely considered. As the intermediary system, it was proposed to use photons in an optical fibrr for the case of the QST between two quantum dots placed inside two microcavities connected through the optical fibre [1–4], or a network of interacting spins in the case of the QST between two spin-qubits interacting with this network [5–17] (for a list of references, see the review of Bose [10]). It is known that the perfect QST from one end of a homogeneous N-qubit chain to another is possible only for N=2 and 3 [7]. In order to achieve the perfect QST, it was proposed to use engineered spin chains with untunable but modulated coupling between adjacent spins, and a special version of engineered spin chains that allowed the perfect QST to be found in [7].
The purpose of this work was to establish a wide class of engineered inhomogeneous mirror-symmetric N-spin chains with modulated untunable couplings that can provide the perfect QST between two ends of each chain. It includes as special cases the spin chains proposed in [7]. In section 2, the conditions sufficient for the engineered mirror-symmetric spin chains allowing the perfect QST are derived. From these conditions, the algebraic equations determining the physical parameters of these spin chains are established. By solving these equations, we can obtain the sets of values of these physical parameters. Examples of the chains with even numbers of spins are presented in section 4, and those with odd numbers of spins are presented in section 5. Section 6 is the conclusion.
2. General conditions for the perfect quantum state transfer through mirror-symmetric spin chains
Following the idea in [8, 9], we have studied mirror-symmetric engineered inhomogeneous N-spin chains. The Hamiltonian of each chain is invariant under its mirror inversion I through the centre of this chain. In the Hilbert space of state vectors of a chain of N spins, we introduce basis vectors |i1 i2 ... iN 〉, where the index in labels the quantum state of nth spin, in =0 for its ground state and in =1 for the excited state. N basis vectors of the form
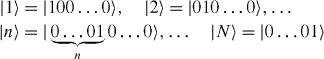
are state vectors of the quantum states with the excitation of only one spin—single excitation states. The mirror inversion I has following action on these state vectors

Consider first a chain of an even number of spins, N=2N0, N0 being an integer. Instead of the basis vectors |n〉 in the Hilbert subspace V(1)of state vectors of single excitation states, it is convenient to use symmetric and antisymmetric normalized combinations,
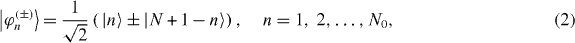
as the basis vectors of V(1). Each set of unit vectors | φn (+)〉 or | φ n (−)〉 spans a N0-dimensional vector subspace V(+) or V(−), respectively, of V(1). Each of them is invariant under the mirror inversion, | φ n (+)〉 are the even state vectors while | φ n (−)〉 are the odd ones:
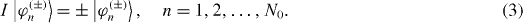
V(1) is decomposed into the direct sum of V(+) and V(−).
The mirror symmetry of the spin chain means that each vector subspace V(+) and V(−) is invariant with respect to the action of the Hamiltonian

In each vector subspace, V(+) or, V(−) there are N0 eigenvectors | ψk (+)〉 or | ψ k (−)〉 of H:
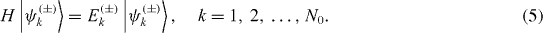
Each of them is a linear combination of N0 unit vectors (

Coefficients Akn (±) satisfy the following conditions:


and therefore formula (

In order to study the transfer of the excitation from one spin of the chain to another, we now consider the time evolution of the state vector of a single excitation state |n〉. Using formulae (
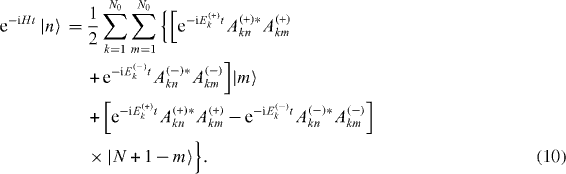
Suppose that eigenvalues Ek ( ±), k=1,2, ...,N0 can be expressed in the form

with some value E0 of energy, some value τ of time and arbitrary integers νk
and μk
. From equations (

This means that, up to a common phase factor e
−i
E0τ, the dynamical evolution of the chain during the time interval τ leads to the mirror inversion (
In the case of a chain of an odd number of spins, N=2N0+1, as well as mirror-symmetric and mirror-antisymmetric state vectors (

Invariant basis vector | φ N0+1(+)〉 and N0 mirror-symmetric state vectors | φ n (+)〉, n=1, 2,...,N0, span a (N0+1)-dimensional vector subspace V(+) invariant with respect to the action of Hamiltonian H. Each of (N0+1) eigenstates | ψ k (+)〉 of H in V(+),
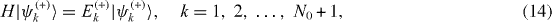
is a linear combination of (N0+1) unit vectors |φ n (+) 〉

Mirror-antisymmetric state vectors |φ n (−) 〉, n=1, 2,...,N0, are basis vectors of a N0-dimensional invariant vector subspace V(−). Each eigenstate of |ψ k (−) 〉 of H in V(−),

can be expressed in the form
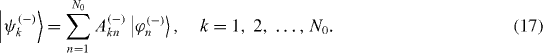
Instead of formulae (
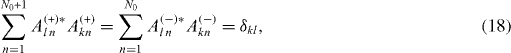

and instead of formula (
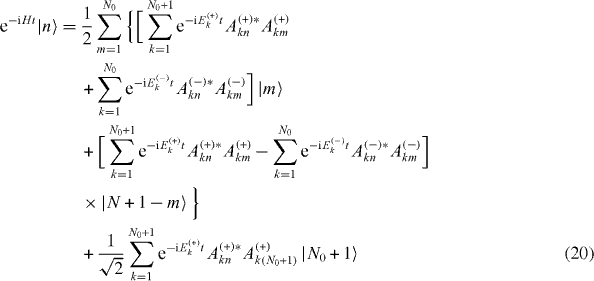
for n≤N0, and

Suppose that (N0+1) eigenvalues Ek
(+) and N0 eigenvalues Ek
(−) are determined by formulae (

with n≤N0, and

This means that, up to a common phase factor e
−
i
E0 τ, the dynamical evolution of the chain during the time interval τ leads to the mirror inversion (
Thus, we can conclude that in mirror-symmetric spin chains the perfect QST can take place if the eigenvalues Ek
( ±) of their Hamiltonians satisfy sufficient conditions (
3. Algebraic equations determining physical parameters of engineered spin chains allowing perfect quantum state transfer
In order to satisfy sufficient conditions (
Consider first a chain of an even number N=2N0 of interacting spins with the Hamiltonian of the form
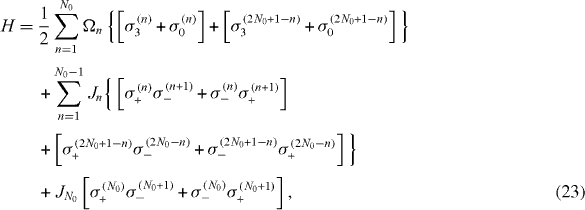
where N0 energy values Ωn
and N0 coupling constants Jn
, n=1, 2,... , N0 are the physical parameters to be determined, σα
(n) with α=0 3, ± are the 2×2 unit matrix and the matrices σ3, σ± acting on the state vector of the nth spin. From the Schrödinger equation (

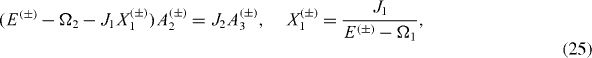
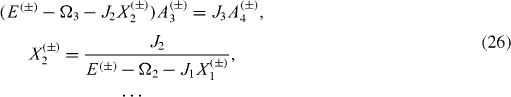
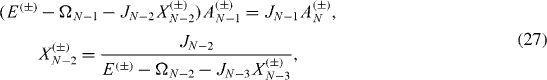
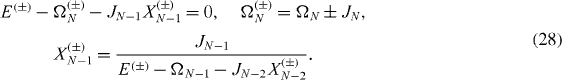
The system of algebraic equations (
In the case of a chain consisting of an odd number N=2N0+1 of interacting spins, we have the Hamiltonian of the form
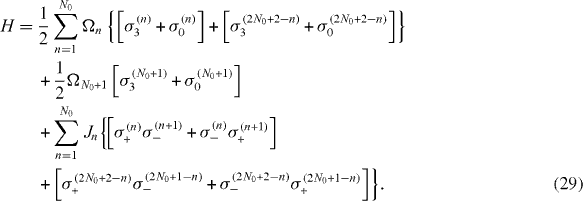
where (N0+1) energy values Ωn
, n=1, 2,..., N0+1, and N0 coupling constants Jn
, n=1, 2,...,N0, are the physical parameters to be determined. From Schrödinger (

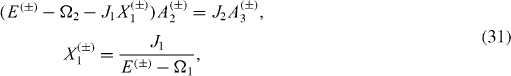
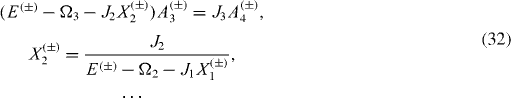
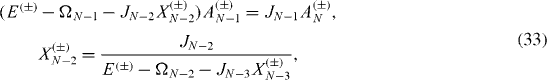
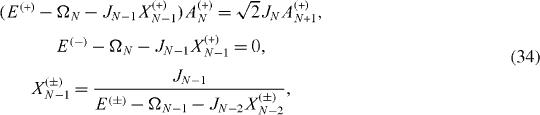
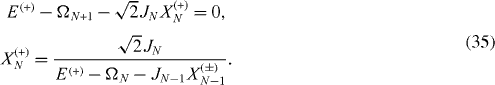
Equations (
As in the previous case, the system of algebraic equations (
4. Examples of chains with even numbers of spins: N=2N0
4.1. N0=1: two-spin-chain
It is known that a system of two identical interacting spins allows the perfect QST (see, for example [7, 18]). The Hamiltonian of this system contains two physical parameters Ω, J and has two eigenstates,

with the corresponding eigenvalues of H:

In this case, formulae (

with integers ν and μ. From equations (

with some integers λ.
The dynamical time evolution of the excited states |1〉 and |2〉 of two spins is described by the following expressions:
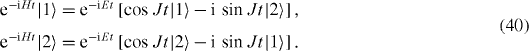
They show that the perfect QST takes place at the time moments τ determined by equation (
4.2. N0=2: four-spin-chain
In a mirror-symmetric four-spin-chain, there are four physical parameters Ω1, Ω2 and J1, J2. The Hamiltonian has four eigenstates with four eigenvalues:

Considering formulae (
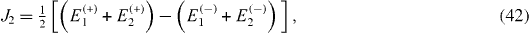
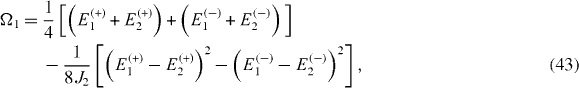
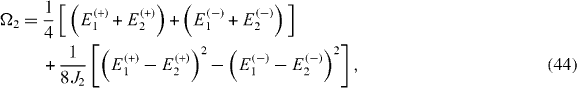
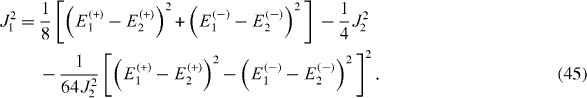
Formulae (
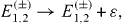
while Ω1 and Ω2 are shifted by the same amount:
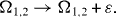
All mirror-symmetric four-spin-chains with physical parameters determined by equations (
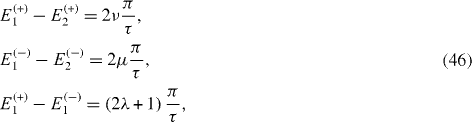
with some integers ν, μ and λ, and we have


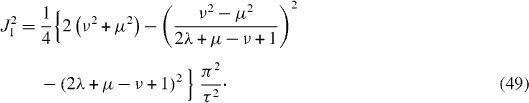
In the special case ν=μ=2λ+1 from equations (
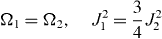
in agreement with the result of Christandl et al [7] for a four-spin-chain.
4.3. N0=3: six-spin-chain
In a mirror-symmetric six-spin-chain, there are six physical parameters Ω1, Ω2, Ω3 and J1, J2, J3. The Hamiltonian has six eigenstates with six eigenvalues Ek ( ±), k=1, 2, 3. They are related to six physical parameters through the six following equations:
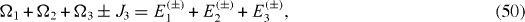
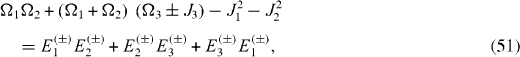
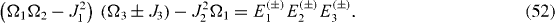
By solving this system of six algebraic equations, we derive the expressions of physical parameters Ωn and Jn , n=1, 2, 3, in terms of six eigenvalues Ek ( ±), k=1, 2, 3:

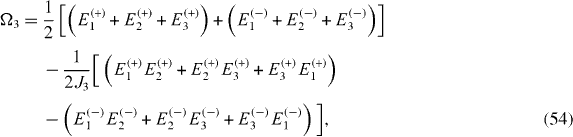
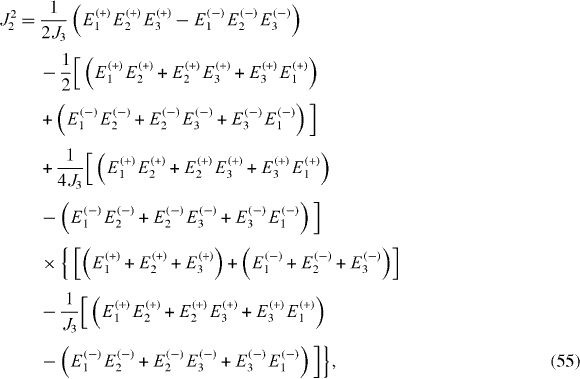
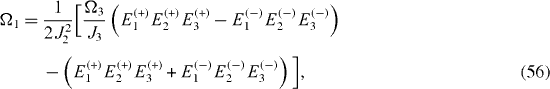
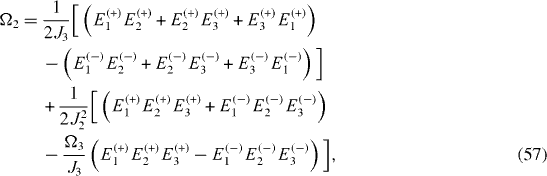

The perfect QST is ensured if the eigenvalues Ek
( ±), k=1, 2, 3, satisfy conditions (
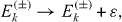
k=1, 2, 3, while all parameters Ω1, Ω2, Ω3 are shifted by the same amount
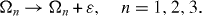
In [7], it was shown that the perfect QST is possible through a six-spin-chain with the following physical parameters:
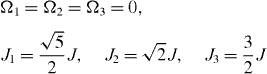
with some constant J. It is easy to check that, for this six-spin-chain, six eigenvalues Ek
( ±), k=1, 2, 3, have the expressions of the form (
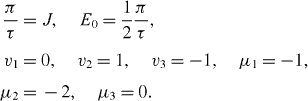
This means that the six-spin-chain found in [7] is a special case of a wide class of six-spin-chains satisfying sufficient conditions (
The reasoning presented above can be applied to other chains with even numbers of spins.
5. Examples of chains with odd numbers of spins: N=2N0+1
5.1. N0=1: three-spin-chain
It is known that a system of three identical interacting spins allows the perfect QST (see [7]). Here, we consider a mirror-symmetric three-spin-chain with two energy parameters Ω1, Ω2 and one coupling constant J. It has three eigenstates | ψ k (+)〉, k=1, 2 and | ψ k (−)〉 with eigenvalues

and

Conditions (
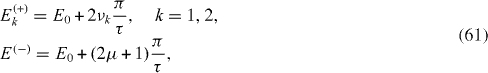
with integers ν 1, ν 2 and μ.
The dynamical time evolution of the excited states |1〉 and |3〉 of two spins at two ends is described by two similar formulae:
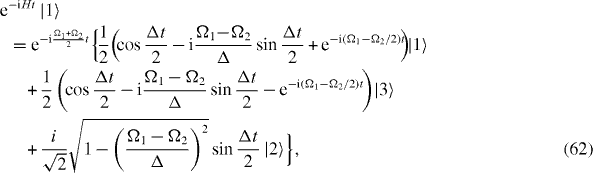
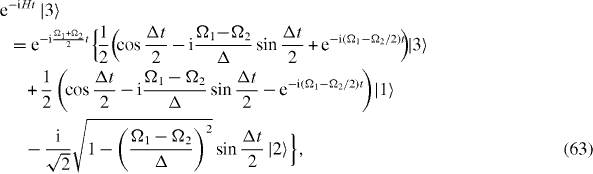
while that of the excited state |2〉 is described by the following expression:
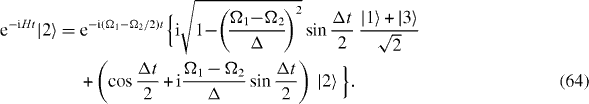
In the special case Ω 1=Ω 2, formulae (
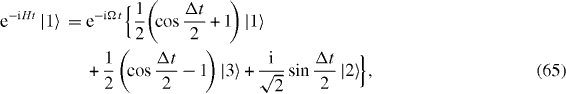
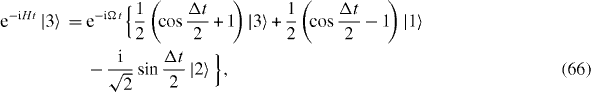
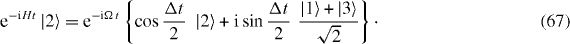
Formulae (
5.2. N0=2: five-spin-chain
The Hamiltonian of a mirror-symmetric five-spin-chain contains five physical parameters: three energy values Ω1, Ω2, Ω3 and two coupling constants J1, J2, and has five eigenstates with five eigenvalues: Ek (+), k=1, 2, 3 and El (−), l=1, 2. From the Schrödinger equations for the eigenstates, it follows a system of five equations determining five eigenvalues in terms of five physical parameters and vice versa:
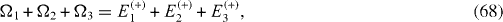

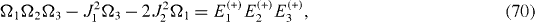

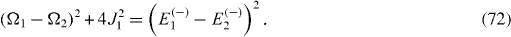
By solving the systems of equations (
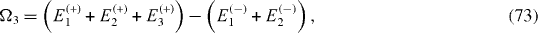
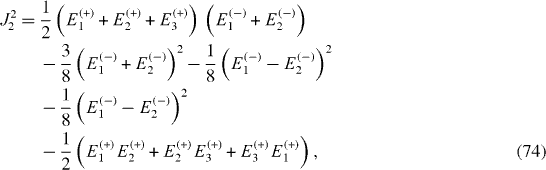
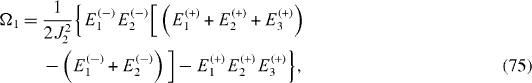
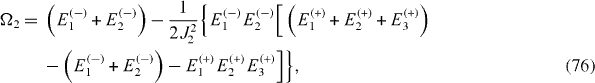

By means of lengthy algebraic calculations, it can be shown that the expressions of coupling constants J1, J2 are invariant with respect to the shift of all energy levels Ek (+), k=1, 2, 3 and El (−), l=1, 2 by one and the same quantity
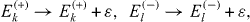
while all energy values Ω1, Ω2, Ω3 are shifted by the same amount:
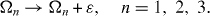
Formulae (
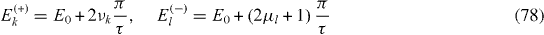
determine the sets of values of physical parameters of mirror-symmetric five-spin-chains allowing the perfect QST. A special case of this class of five-spin-chains was found in [7]:
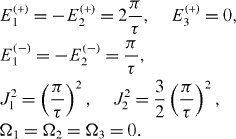
5.3. N0 =2: seven-spin-chain
The Hamiltonian of a mirror-symmetric seven-spin-chain contains seven physical parameters: four energy values Ω1, Ω2, Ω3, Ω4 and three coupling constants J1, J2, J3, and has seven eigenstates with seven eigenvalues: Ek (+), k=1, 2, 3, 4 and El (−), l=1, 2, 3. From the Schrödinger equations for the eigenstates, it follows a system of seven equations determining seven eigenvalues in terms of seven physical parameters and vice versa:
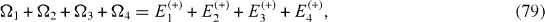
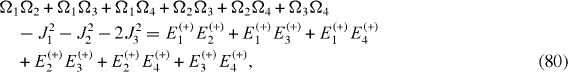
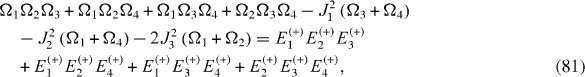
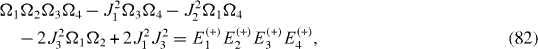
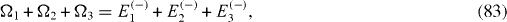

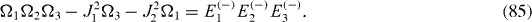
By solving the systems of equations (
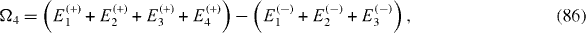
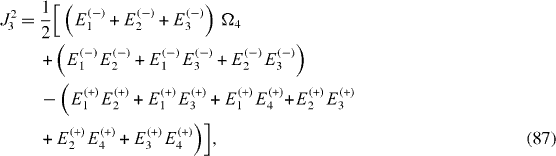
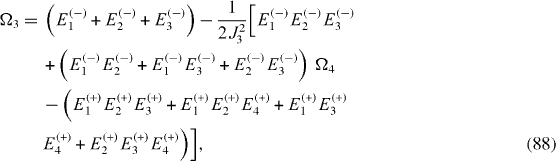

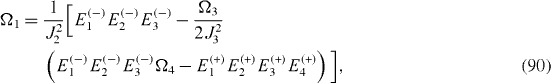

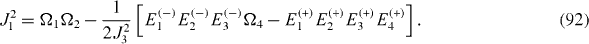
It can be shown that the expressions of coupling constants J1, J2, J3 are invariant with respect to the simultaneous shift of all energy levels Ek (+), k=1, 2, 3, 4 and El (−), l=1, 2, 3 by one and the same quantity,
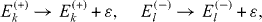
while all energy values Ω1, Ω2, Ω3, Ω4 are simultaneously shifted by the same amount:
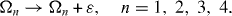
Formulae (
The reasoning presented above can be applied to other chains with odd numbers of spins.
6. Conclusion
The transfer of the excited state along the chains of N spins with the XY Heisenberg exchange interaction between nearest-neighbour spins and without decoherence was studied. It was shown that there exists a wide class of mirror-symmetric engineered N-spin-chains allowing the perfect QST. The Hamiltonian of each chain of N spin of this class depends on N physical parameters and has N eigenvalues. The physical parameters are expressed in terms of the eigenvalues. If the eigenvalues satisfy sufficient conditions of the form (
Acknowledgments
This work was completed in the Max-Planck Institute for the Physics of Complex Systems MPI-PKS, Dresden, Germany. The authors would like to express their gratitude to MPI-PKS for their hospitality and to Professor Peter Fulde for encouragement. We thank the Vietnam Academy of Science and Technology for their support.
