Translational motion of an atom in a weakly driven fiber-Bragg-grating cavity

Strong coupling between an atom and a cavity field occurs when the maximal atom–field dipole coupling strength exceeds the cavity field decay rate and the atomic spontaneous emission rate [1]. In this regime, excitations can be exchanged coherently between the atom and the field several times before the incoherent decay process occurs, the properties of the field can be significantly modified by the presence of even a single atom, and the presence of a single photon in the field can saturate the response of the atom. The effects of single atoms on the cavity field in real time [2, 3] have been observed [4–6]. It has been reported that the presence of an atom in the cavity, which is tuned to the atomic transition and resonantly driven by a laser field, can lead to a dramatic drop in the transmitted intensity [4].

Due to recent developments in taper fiber technology, thin fibers can be produced with diameters down to 50 nm [7]. Subwavelength-diameter vacuum-clad silica-core fibers are called nanofibers. Several methods for trapping and guiding neutral atoms outside a nanofiber have been proposed and studied [8–14]. Efficient channeling of emission [15] from a few atoms into guided modes has been realized [16]. Thin fiber structures can be used as building blocks in future atom and photonic micro- and nanodevices. Thin fibers can also be used as efficient nanoprobes for atoms, molecules and quantum dots.

Recently, it has been proposed to combine the cavity technique with the nanofiber technique to obtain a hybrid system: a nanofiber with two built-in fiber-Bragg-grating (FBG) mirrors [17]. In this system, the FBG mirrors form a fiber cavity transmitting and reflecting the guided field of the nanofiber. Such a hybrid system is interesting because the interaction between the field and the atoms in the vicinity of the fiber is enhanced not only by the transverse confinement of the field in the fiber cross-section plane but also by the longitudinal confinement of the field between the mirrors. An advantage of a FBG cavity based on a nanofiber is that the field in the guided modes can be confined to a small cross-section area whose size is comparable to the light wavelength. Another advantage of the nanofiber-based cavity is that the cavity guided field can be transmitted over long distances for communication purposes. The nanofiber-based cavity can find applications in the merged areas of fiber optics, cavity quantum electrodynamics, and ultracold neutral atoms. It has been shown that the presence of a FBG cavity with a large length (on the order of 10 cm) and a moderate finesse (about 30) can significantly enhance the group delay of a guided probe field [17] and substantially enhance the channeling of emission from an atom into a nanostructure [18]. The effect of an atom on a quantum guided field in a weakly driven FBG cavity has been studied [19].

When an atom is in the close vicinity of a nanofiber, it undergoes the van der Waals force from the fiber surface. In addition, since the guided modes have the evanescent-wave behavior on the outside of the fiber, the optical force from the guided field upon the atom can be significant. The total force governs the atomic motion and hence modifies the guided field through the spatially dependent atom–field coupling. It is necessary to study the force and the atomic motion in order to find ways to effectively control and manipulate the atom–field interaction in the nanofiber-based cavity.

In this article we study the translational motion of an atom in the vicinity of a weakly driven nanofiber with two FBG mirrors. We show that the time development of the mean number of photons in the cavity closely follows the translational motion of the atom even though the cavity finesse is moderate, the cavity is long, and the probe field is weak.

The article is organized as follows. In section 2, we describe the model. In section 3, we calculate the force on a motionless atom and the friction coefficients. In section 4, we study the momentum diffusion. In section 5, we examine the center-of-mass motion of the atom. Our conclusions are given in section 6.

We consider a two-level atom in the vicinity of a nanofiber with two FBG mirrors (see figure 1). The field in the guided modes of the nanofiber is reflected back and forth between the FBG mirrors. The nanofiber has a cylindrical silica core of radius a and of refractive index n₁=1.45 and an infinite vacuum clad of refractive index n₂=1. In view of the very low losses of silica in the wavelength range of interest, we neglect material absorption. We use the cylindrical coordinates (r,φ ,z), with z being the axis of the fiber.

Zoom In Zoom Out Reset image size

In order to describe the field in a quantum-mechanical formalism, we follow the continuum field quantization procedures presented in [20]. First, we temporally neglect the presence of the FBG mirrors. In the presence of the fiber, the electromagnetic field can be decomposed into guided and radiation modes [21]. The guided modes have the evanescent behavior on the outside of the core. They can travel in the waveguide without loss of power, provided that losses in the dielectric material are ignored. Meanwhile, the radiation modes are oscillatory at large distances from the fiber and do not have the evanescent behavior. They cannot be normalized with respect to a finite amount of power. Regarding the guided modes, we assume that the single-mode condition [22] is satisfied for a finite bandwidth around the atomic transition frequency ω ₀. We label each fundamental guided mode ^HE ₁₁ in this bandwidth by an index (ω ,f,l), where ω is the frequency of the mode, f=+,− denotes the forward or backward propagation direction and l=+,− stands for the counterclockwise or clockwise rotation of polarization. The propagation constant β=β (ω) of a guided mode is determined by the fiber eigenvalue equation [21].

Next, we take into account the effect of the FBG mirrors on the mode functions. We assume that the two FBG mirrors are identical, having the same complex reflection and transmission coefficients R and T, respectively, for the guided modes in a broad bandwidth around the atomic transition frequency ω ₀. Without loss of essential physics, we assume that the gratings are lossless, that is, |R|²+|T|²=1. Let the mirrors be located at the positions z=±L/2 along the fiber, where L is the distance between the mirrors. The mode functions of the cavity-modified guided modes are obtained, as usual in the Fabry–Perot theory, by summing the geometric series resulting from the multiple reflections by the mirrors. We assume that the FBG mirrors do not reflect the radiation modes.

We drive the FBG cavity by a classical probe light field propagating along the fiber in a guided mode μ ^_p =(ω ^_p ,f ^_p ,l ^_p ). Let P ^_in be the incident power. The power of the transmitted field is given by , where is the mean intracavity photon number and κ=(1−|R|²)v ^_g /L|R| is the cavity damping coefficient. In the absence of the atom, the mean number of photons in the cavity is , where Δ ^_c =ω ^_p −ω ^_c is the detuning of the probe field from the cavity resonance and η=(κP ^_in /2ℏω ^_p )^1/2 is the cavity pumping rate. We assume that the probe field excites a single fiber-guided cavity mode (ω ^_c ,f ^_c ,l ^_c ), where f ^_c =f ^_p and l ^_c =l ^_p . Furthermore, we assume that the probe field and the cavity field are counterclockwise circularly polarized, that is, l ^_p =l ^_c =+, and that the atomic transition is σ+ polarized.

In the vicinity of the fiber surface, the atom experiences the effects of the van der Waals potential on the internal state energy and on the center-of-mass motion. Let V ^_g and V ^_e be the van der Waals potentials for the ground state |g〉 and the excited state |e〉, respectively. In the presence of the fiber, the atomic transition frequency is shifted from the bare frequency ω ₀ and is given by ω ^_a (r)=ω ₀+V ^_eg (r)/ℏ, where V ^_eg =V ^_e −V ^_g . It is clear that the effect of the van der Waals potential on the atomic transition frequency is negligible in the region of large distances r–a but significant in the region of small distances r–a. In our numerical calculations, we assume for simplicity that the van der Waals potential from the fiber is the same as that from a flat surface, that is, V_α=−^C _3α /(r−a)³, where α=g,e.

It has been shown that the interaction between the atom and the fiber-guided cavity field can be described in the interaction picture by the effective Hamiltonian [19]

Here p and M are the momentum and the mass of the atom, respectively, Δ ^_a =ω ^_p −ω ^_a is the detuning of the probe field frequency ω ^_p from the shifted atomic transition frequency ω ^_a , and

is the atom–cavity coupling coefficient [19]. The notations a and a^† stand for the cavity photon operators. The operator σ _z =|e〉 〈e|−|g〉 〈g| characterizes the atomic population inversion. The notations σ=|g〉 〈e| and σ ^†=|e〉 〈g| stand for the atomic downward- and upward-transition operators, respectively. In expression (2), the parameter d is the matrix element of the electric-dipole moment of the atom, and e ^{_r (ω _c )} and e_φ ^{(ω _c )} are the radial and azimuthal components of the normalized guided-mode profile function [15, 21]. We have assumed for simplicity that the order of the cavity resonance is even, that is, the center of the cavity corresponds to an antinode of the cavity standing-wave field.

The equation for the mean value 〈 ^O〉 of an arbitrary observable ^O is

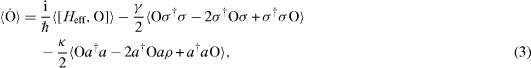
where γ is the decay rate of the atom in the presence of the nanofiber. Hence, we find

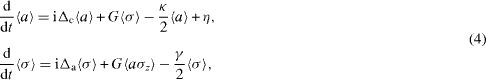
and

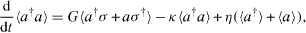
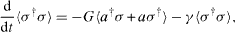
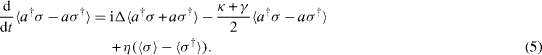
Here Δ=ω ^_c −ω ^_a is the cavity–atom detuning.

To obtain some simple analytical results, we consider the case where the probe field is so weak that the excited state is hardly occupied and that there is at most one photon in the cavity. In this case, we can linearize equations (4) and (5) by using the approximations 〈aσ _z 〉=−〈a〉 and 〈a^† aσ _z 〉=−〈a^† a〉. When we solve the resulting equations in the steady-state regime, we obtain [23]

and

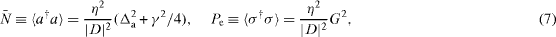
where

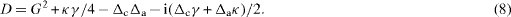
Since the parameters, G, γ and Δ ^_a vary in space, the intensity of the transmitted light depends on the position of the atom.

The total force F on an atom is defined as

We find from equations (1) and (9) the expression

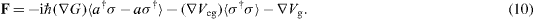
Note that, due to the cylindrical symmetry of the atom–field interaction, the azimuthal component F_φ of the force is zero. Consequently, the total force F in the cylindrical coordinates has only two components, F_r and F_z .

3.1. Force on a motionless atom

We consider the case where the atom is motionless or its center-of-mass motion is very slow. In this case, the internal state of the atom–field system can be approximated by the local steady state. Using this state, we can calculate the force F⁽⁰⁾ on a motionless atom. We find

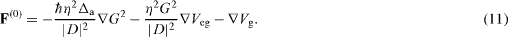
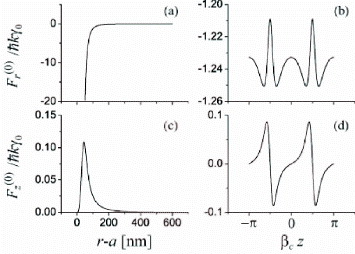
In figure 2, we plot the results of the numerical calculations for the radial component F ^{_r (0)} and the axial component F_z ⁽⁰⁾ of the force on a motionless atom. The FBG cavity length is L=10 ^cm. The FBG mirror reflectivity is |R|²=0.9, which corresponds to the finesse F=π |R|/(1−|R|² ) ≅ 30, a moderate value. The parameters of the atom correspond to the D₂-line transition of cesium, with the wavelength λ ₀=852 ^nm and the natural linewidth γ ₀ /2π=5.25 ^MHz. For the parameters used, we find the atom-cavity coupling coefficient G(r,z)|_r=a,z=0=5.33γ ₀, the cavity damping rate κ=7.02γ ₀, and the atomic decay rate γ (r)|_r=a =1.73γ ₀. It is clear that the strong-coupling condition 2|G|> κ, γ is satisfied when the atom is close to the fiber and to an antinode of the cavity standing-wave field. The input probe power is P ^_in =1 ^pW. For the parameters used, the mean number of intracavity photons in the absence of the atom is very small, namely, in the case of figure 2. We observe from the figure that the spatial dependence of the force is rather complicated. One reason is that the coupling between the atom and the fiber-guided cavity field is periodic in the axial direction and has the evanescent-wave nature in the radial direction. Another reason is the presence of the van der Waals potential, which not only leads to the van der Waals force but also affects the optical force through the shift of the atomic transition frequency. Figure 2(a) shows that in the close vicinity of the fiber surface (r−a< 100 ^nm), the radial component F_r ⁽⁰⁾ of the force varies quickly and is negative as it is mainly determined by the spatial gradient of the van der Waals potential in this region. For large distances r–a, the radial force component F_r ⁽⁰⁾ is mainly determined by the spatial gradient of the coupling between the atom and the fiber-guided cavity field. We observe from figure 2(d) that the axial component F_z ⁽⁰⁾ of the force changes its sign at the nodes (β _c z=± π /2, ± 3π /2, ...) and antinodes (β _c z=0, ± π , ± 2π , ...) of the cavity standing-wave field.

Zoom In Zoom Out Reset image size

3.2. Friction force

In general, the force F on the atom depends on the atomic velocity v=(^v _r ,v_φ ,v_z ) due to the Doppler shift of the atomic transition frequency and the gradient of the field. To calculate the effect of a small velocity v on the force, we perform a simple linearization procedure [24]. For a moving atom, the total force is

where F⁽⁰⁾ is the force on a motionless atom and F⁽¹⁾ is the friction force. We can present the components F_i ⁽¹⁾, with i=r,φ ,z, of the friction force F⁽¹⁾ in the form

Here β _ij with i,j=r,φ ,z are the friction coefficients. Due to the cylindrical symmetry, we have β _ⁱφ=β _φⁱ =0.

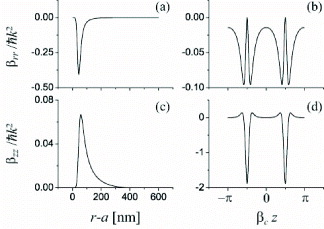
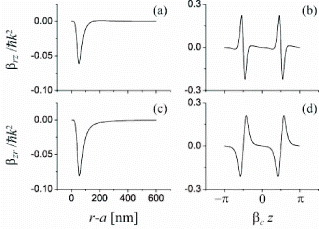
We calculate numerically the friction coefficients β _ij . We plot the radial and axial friction coefficients β _rr and β _zz in figure 3 and plot the cross friction coefficients β _rz and β _zr in figure 4 for the parameters of figure 2, where the probe field, the cavity, and the atom are at exact resonance, that is, ω ^_p =ω ^_c =ω ₀. We observe from figures 3 and 4 that the spatial dependences of the friction coefficients are complicated. Depending on the atom-to-surface distance and on the detuning, the friction coefficients can be positive or negative.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The atomic momentum spread is characterized by the diffusion coefficient

This coefficient can be given by the integral of force correlations

Here the quasi-stationary conditions have been assumed and the notation has been introduced.

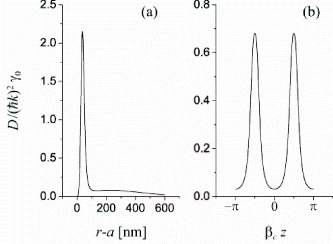
We again consider the case where the probe field is so weak that the excited state is hardly occupied and there is at most one photon in the cavity. We plot the diffusion coefficient D in figure 5 for the parameters of figure 2. Figure 5(a) shows that D has a peak when the atom-to-surface distance r−a is small enough but not too small. The appearance of such a peak is a result of the balance between the competing effects of the van der Waals potential and the atom–cavity coupling.

Zoom In Zoom Out Reset image size

The classical motion of the center of mass of the atom is governed by the equations

Here M is the mass of the atom, F_r , F_φ, and F_z are the cylindrical-coordinate components of the force F, and , and are the random variables that characterize the momentum diffusion.

We use the method of [6] to solve equations (16). In every time step Δt of the numerical integration of p, a stochastic term is added. Here , and are the unit vectors for the cylindrical coordinates r, φ and z, respectively. The quantity ^R _j (p), where j=r,φ ,z, produces a random number between - p and p. The coefficients D_r , D_φ and D_z are the cylindrical-coordinate components of the diffusion coefficient D=D_r +D_φ+D_z , which are responsible for the motion along the , and directions, respectively.

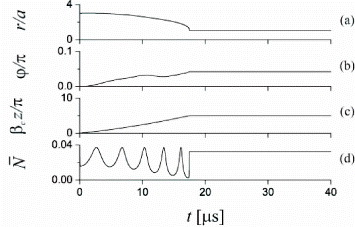
We plot in figure 6 the time dependences of the atomic position (r,φ ,z) and the mean intracavity photon number . In these calculations, we assume that the initial velocity of the atom is aligned along the direction z of the fiber axis and that the atom stops moving after it reaches the fiber surface. Figure 6(c) shows that the velocity of the atom along the direction z of the fiber axis is almost constant. The reason is the following: since the probe field is weak and is at exact resonance with the cavity and the atom, the optical force is small. Consequently, the translational motion of the atom in the case of figure 6 is mainly determined by the van der Waals force, which acts only in the radial direction. Figure 6(d) shows that the mean intracavity photon number oscillates in time, with peaks and dips at the nodes and antinodes of the cavity standing-wave field, respectively. Such oscillations closely follow the motion of the atom through the nodes and antinodes of the cavity field.

Zoom In Zoom Out Reset image size

We have calculated numerically and analytically the force, the friction coefficients, and the momentum diffusion. We have found that the spatial dependences of the force, the friction coefficients, and the momentum diffusion are very complicated due to the evanescent-wave nature of the atom-field coupling and the effect of the van der Waals potential. We have shown that the time development of the mean number of photons in the cavity closely follows the translational motion of the atom through the nodes and antinodes of the fiber-guided cavity standing-wave field even though the cavity finesse is moderate, the cavity is long, and the driving-field power is very weak.