Quantum dynamics of quantum bits

The most fundamental element for encoding quantum information (QI) in all quantum systems for QI processing is the quantum bit (qubit)—the quantum analogue of the (classical) bit in computer science. Any two-state quantum system can be used as a qubit and its wave function or density matrix is the QI encoded into this qubit [1, 2]. The interactions between qubits as well as the interactions of qubits with other quantum systems are the physical origins of the mechanisms of QI transfer or transmission from one qubit to another [3–13]. In general, the principles of QI processing mechanisms were found on the basis of the study of the quantum dynamics of qubits and qubit systems.

The present work is a review of fundamental problems of the quantum dynamics of qubits and their interactions. The general formalism is presented in section 2, then it is applied to the study of free qubits in section 3. The quantum dynamics of qubits in a pumping classical radiation field is studied in section 4. Section 5 is devoted to the study of the decoherence of a qubit due to its interaction with a dissipative environment. The strongly coupled quantum system consisting of a two-level quantum dot (QD) as a qubit interacting with the quantum electromagnetic field in a single-mode microcavity (MC) without decoherence is studied in section 6. The effects of the decoherence in the last quantum system are also discussed. The conclusion and discussion are presented in section 7.

Any two-state system can be used as a qubit. If it is an isolated system, then in the Schrödinger picture its quantum statistical states are described by a t-dependent 2×2 density matrix ρ(t). In the Hilbert space of the state vectors of this system, we can use any pair of two orthogonal and normalized vectors |i〉, i=1, 2,

as the basis. Then the density matrix ρ(t) is expressed in the form

with the matrix elements

Introduce the fermionic destruction and creation operators c_i and c_i ⁺, i=1, 2, satisfying the canonical anticommutation relations,

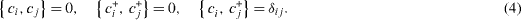
as well as the vacuum state vector | 0 〉 satisfying the condition

and define

It follows that

and therefore the matrix elements (3) can be expressed in the form

In general, there always exists the interaction between the qubit and the environment. The matrix elements of the total density matrix ρ ^_tot (t) of the complex system consisting of the qubit and the environment depend on the degrees of freedom of both the qubit and the environment. The trace of the total density matrix ρ ^_tot (t) over the degrees of freedom of the environment,

is called the reduced density matrix for the qubit. Being an operator in the Hilbert subspace of the state vectors of single fermions c_i , it describes the states of the qubit in the presence of its interaction with the environment and has the matrix elements

where ^Tr _S denotes the trace over the degrees of freedom of the qubit. Substituting expression (9) into the rhs of equation (10), we obtain

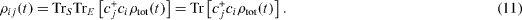
The total density matrix ρ ^_tot (t) satisfies the quantum Liouville equation (also called the von Neumann equation) with the total Hamiltonian H ^_tot ,

The solution of this equation can be represented in the form

where U(t) is a unitary operator in the Hilbert space of the total system. It is determined by the equation

and the initial condition

Substituting expression (13) into the rhs of formula (11), we rewrite this formula in the form

where

are the destruction and creation operators in the Heisenberg picture. They obey the quantum Heisenberg equations of motion,

Denote 〈A(t) 〉 as the statistical average value of the operator A(t) in the statistical state with the t-independent density matrix ρ(0),

Then formula (16) is rewritten in the form

From the quantum Heisenberg equations (18), it follows that

In practice, the total Hamiltonian H ^_tot can always be divided into two parts,

such that one part H ^_coh describes the coherent quantum dynamics of a non-interacting system consisting of the qubit and other quasi-particles in the environment while the second part H ^_dis is the Hamiltonian of the interaction of the qubit with the environment and causes the dissipation of the coherent excitations in the subsystem with the Hamiltonian H ^_coh . The time derivative of the matrix elements ρ_ij (t) is also divided into two parts,

where

is generated by the coherent quantum dynamics with the Hamiltonian H ^_coh and

is caused by the dissipative interaction of the environment.

The results of the study on the dissipation of the two-state system in the spin-boson model were presented in the comprehensive review of Leggett et al [14]. In the Markovian approximation, the contribution of the dissipative interaction of the environment to the time derivative of the matrix elements ρ_ij (t) of the reduced density matrix of any two-state system is expressed in terms of some linear operator called the Liouvillian superoperator L,

The general form of L was exactly derived by Gorini et al [15]. A particular case of the formula of Gorini et al [15] is the Lindblad formula [16, 17]. In the lowest (second) order of the perturbation theory, L is expressed in the form of the Redfield formula [18–20],

with the Redfield tensor R_ijkl having the following hermiticity property,

The subject of the present study is the quantum dynamics of a two-state system as a qubit. To take into account the dissipative influence of the environment, we apply the quantum Liouville equation for the reduced density matrix ρ(t) in the approximate form,

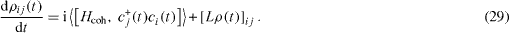
The part H ^_coh of the total Hamiltonian generates the coherent dynamical oscillations of the non-interacting system of the qubit and the bosonic fields. It must contain not only the quantum operators c_i (t) and c_i ⁺(t) of the two-state system but also those of the bosonic quantum fields.

In concluding this section, we note that as a 2×2 matrix, the reduced density matrix ρ(t) can be expanded into a linear combination of the unit matrix σ₀ and three Pauli matrices σ_α, α=1, 2, 3,

or in the explicit form for its matrix elements,

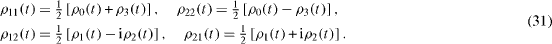
The functions ρ₀(t) and ρ _α (t), α=1, 2, 3 are expressed in terms of the matrix elements ρ_ij (t) of the reduced density matrix,

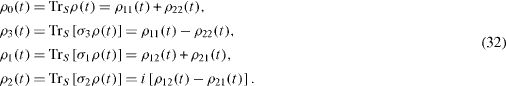
Due to the normalization of the density matrix ρ ^_tot (t) as well as of the reduced density matrix ρ(t),

we always have

The functions ρ _α (t), α=1, 2, 3 can be considered as three components of a vector ρ(t) in a three-dimensional space. Formulae (31) and (32) with condition (34) will be used often in the sequel.

In order to elaborate the calculation method, we start from the simplest example and consider the isolated two-state system with the total Hamiltonian,

which can be used as a free qubit. For the definiteness we suppose that E₁>E₂ and set

It may be a spin 1/2 particle with a non-vanishing magnetic moment in a constant magnetic field (spin qubit) or a double quantum dot consisting of two single-level quantum dots connected one with another by means of the electron tunneling through a potential barrier and containing only one electron (charge qubit). From the total Hamiltonian (35) and the quantum Liouville equation (12) for the density matrix ρ(t), the system of three rate equations follows:

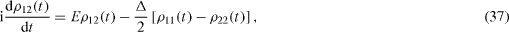
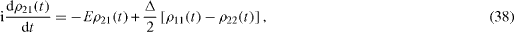
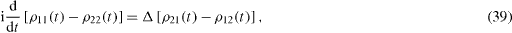
and also the additional equation,

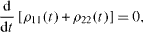
compatible with the normalization condition (34).

It is very easy to solve equations (37)–(39) in the special case Δ=0 and to obtain

In the general case with Δ≠ 0, it is convenient to rewrite the rate equations in the form of differential equations for the components ρ _α (t) of the vector function ρ(t),

By solving this system of three linear first-order differential equations with the given initial values ρ _α (0) of the functions ρ _α (t) at t=0, we obtain

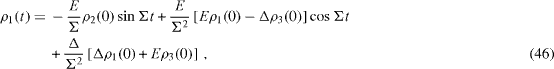
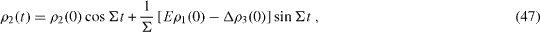
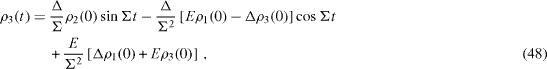
where

The same result can also be derived by means of another method with the use of the Bogolyubov diagonalization procedure. First we rewrite the total Hamiltonian in the diagonal form and then we apply the simple expressions (40)–(42) of the matrix elements of the density matrix of a system with the diagonal total Hamiltonian. Indeed, after the Bogolyubov transformations,

where a, b and a⁺, b⁺ are the destruction and creation operators for new independent fermionic quasi-particles,

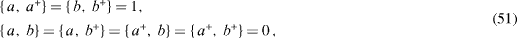
we rewrite the total Hamiltonian in the diagonal form,

with the energy level difference

We introduce the matrix elements of the density matrix of the system with the diagonal Hamiltonian (52)

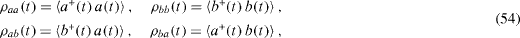
and denote

From formulae (32) and (50), we derive the expression of three components of the vector function ρ(t) in terms of the matrix elements (54),

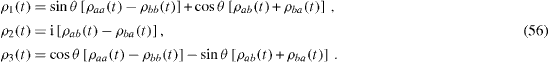
We have shown that for a system with a diagonal Hamiltonian of the form (52) with the energy level difference (53), the density matrix has the matrix elements

The initial values ρ _ab (0),ρ _ba (0),ρ _aa (0)−ρ_bb (0) of the matrix elements (54) are expressed in terms of those of the components of the vector function ρ(t),

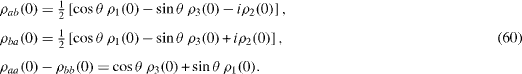
From the relation (56)–(60), it follows that

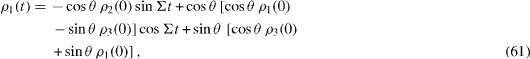
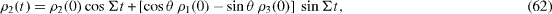
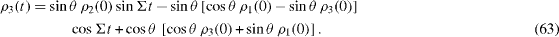
Because

formulae (61)–(63) coincide with the relations (46)–(48).

Besides the two above presented methods, there exists a third one based on the application of the Fourier transformation to the retarded functions,

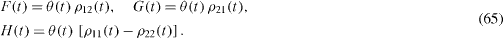
They vanish in the interval t<0, coincide with ρ ₁₂ (t),ρ ₂₁ (t) andρ ₁₁ (t)−ρ ₂₂ (t), respectively, in the interval t>0, and satisfy the following system of inhomogeneous linear first-order differential equations,

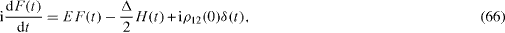
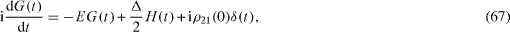
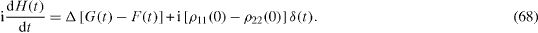
We introduce the Fourier transformation of these retarded functions,

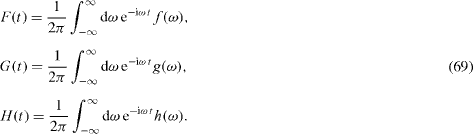
Their Fourier transforms,

are the analytical functions of the complex variable ω in the upper half-plane Im ω>0. From the system of differential equations (66)–(68) follows the system of algebraic equations for the Fourier transforms f(ω ),g(ω) and h(ω),

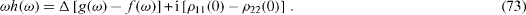
It is easy to solve this system of algebraic equations and to obtain the explicit expressions of h(ω) and the linear combinations f(ω )+g(ω ),ⁱ[f(ω )−^g(ω ) ],

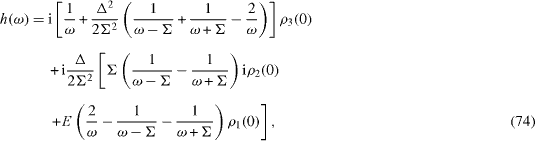
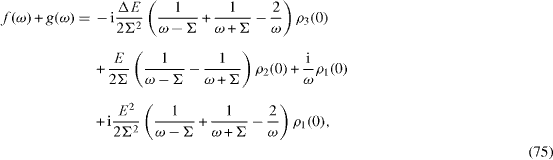
The functions ρ _α (t), α=1, 2, 3 in the interval t>0 are expressed in terms of the Fourier integrals,

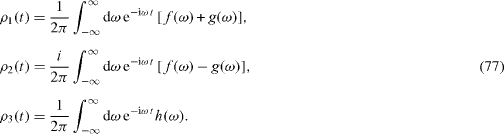
Substituting expressions (74)–(76) into the rhs of formulae (77), we rederive the relations (46)–(48).

Three methods for deriving the explicit expressions of the matrix elements of the density matrix of a free qubit have been presented. All can be applied to the study of the complex systems of the qubits interacting with the environment of bosonic classical and/or quantum fields. For each concrete system, one of these methods might be more efficient than the other two.

Consider now a two-state system as a charge qubit having two energy eigenvalues E_i , i=1, 2,E=E₁−E₂> 0, and interacting with a classical monochromatic radiation field generating the allowed radiative transitions between two levels. The total Hamiltonian has the form

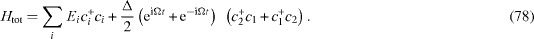
The interaction Hamiltonian consists of two parts. One part gives the resonant contribution to the density matrix at Ω ≈E, while the contribution of the second one has no resonance. Since we shall be interested in the resonance of the coherent oscillations of the qubit under the pumping action of the radiation, we can omit the non-resonant terms and use the following approximate total Hamiltonian,

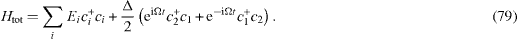
In this case, instead of the system of equations (37)–(39), we have another one,

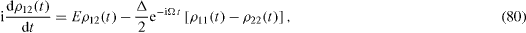
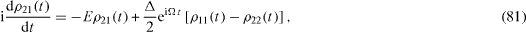
In order to solve this system of linear differential equations, we apply the method based on the use of the Fourier transformation of the retarded functions (65). These satisfy the following inhomogeneous linear differential equations,

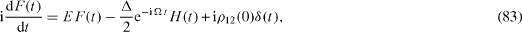
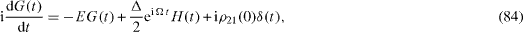
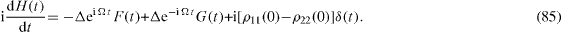
Instead of equations (71)–(73), the Fourier transforms (70) of the functions (65) are determined by following a system of algebraic equations,

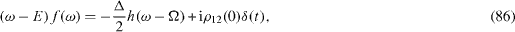
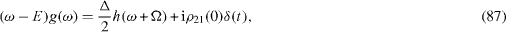
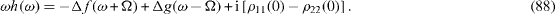
It is easy to solve these equations and to obtain

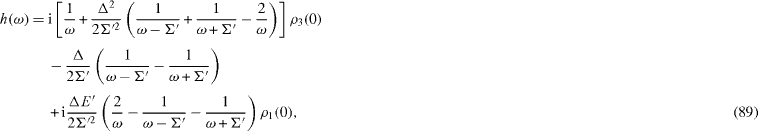
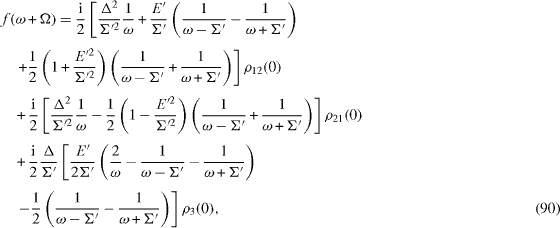
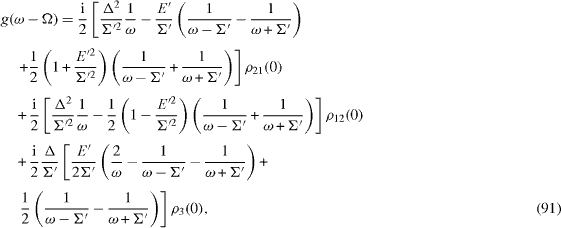
where

By means of the inverse Fourier transformation from expressions (90)–(92), we derive the formulae for the matrix elements of the density matrix,

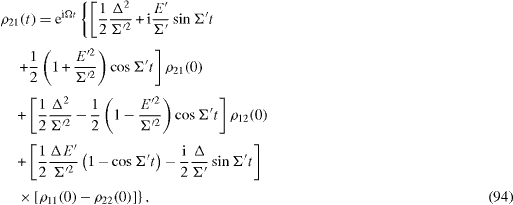
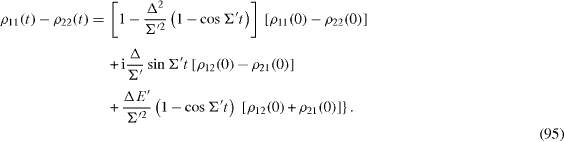
These formulae are the most general expressions of the Rabi oscillations [21]. At the resonance Ω=E,E'=0,Σ '=Δ, they become simple expressions,

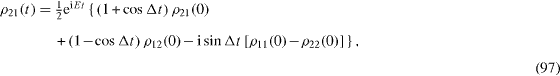
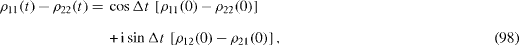
while at Ω=0 they become formulae (46)–(48).

The two-state systems in condensed matter are not the isolated ones but always exist in some environment. Consider now the action of a dissipative environment on the coherent oscillations of the solid-state qubit. In the Born–Markov approximation, the matrix elements (16) of the reduced density matrix of the qubit must obey the rate equations (29). For the generality, we write H ^_coh in the form

which is similar to the Hamiltonian of the interaction of a spin -1/2 particle having a magnetic moment with a magnetic field. Formula (35) with E₁=−E₂ is a special case of this Hamiltonian with E₁ ⁽⁰⁾=Δ, E₂ ⁽⁰⁾=0 and E₃ ⁽⁰⁾=E₁−E₂ . In terms of three components ρ _α (t),α=1, 2, 3 determined by formulae (32), the quantum Liouville equation in the Markovian approximation (29) becomes [22]

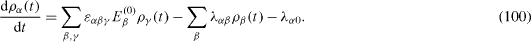
In the Born–Markov approximation, the constants λ _{α β} are expressed in terms of the components of the Redfield tensor as follows:

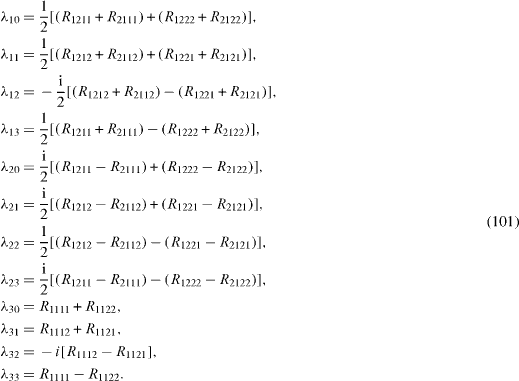
We introduce the constants ρ _α ^∞ satisfying the algebraic equations

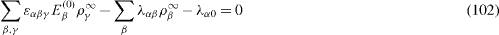
and the functions

It is easy to verify that the functions F_α (t) satisfy the following system of inhomogeneous linear differential equations,

We denote f_α (ω) as the Fourier transforms of F_α (t)

They satisfy the following equations:

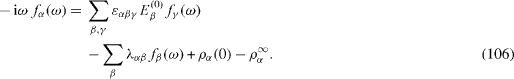
We denote D(z) as the third-order polynomial,

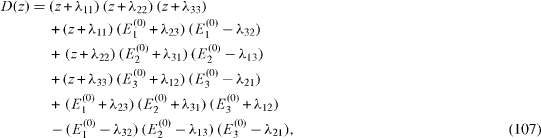
and z₁ ,z₂ and z₃are its three roots,

By solving the system of algebraic equations (106), we derive the explicit expressions of the functions f_α (ω ),α=1, 2, 3,

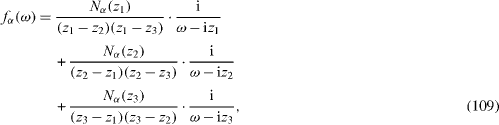
where

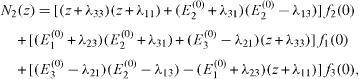
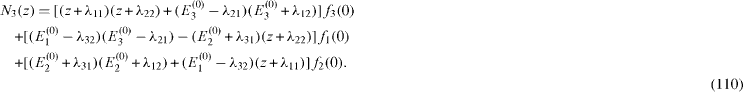
From the general theory on the semigroup of a completely positive Liouvillian superoperator [13–15], it follows that the real parts of the roots z_α must be negative, . Substituting the expressions (109) of the Fourier transforms f_α (ω) into the rhs of formula (105), we derive the following formulae for the functions ρ _α (t),α=1, 2, 3,

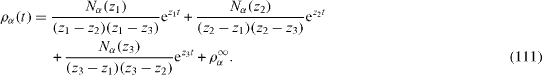
Since λ _{α β} are real constants, the third-order polynomial D(z) can have either one real root z₁ and two complex conjugate roots z₂ and z₃,

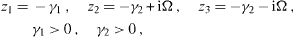
or three real roots,

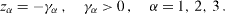
In the former case, the real positive numbers γ ₁ and γ ₂ are the relaxation and dephasing rates and the imaginary parts ± ⁱΩ generate the coherent oscillation with a frequency Ω, while in the latter case there exist three relaxation rates but no oscillation. The difference between Ω and would mean the frequency shift due to the interaction between the qubit and the environment.

Now we study the coherence oscillations in the strongly coupled system consisting of a two-level QD as a qubit and the quantum electromagnetic field in a single-mode MC. This new scientific discipline is called Cavity Quantum Electrodynamics (CQED) [23–30]. In order to have exact eigenstates and eigenvalues of the total Hamiltonian, we assume its approximate Jaynes–Cummings formula [31] which is the quantum extension of the Hamiltonian (79) of the qubit interacting with a classical monochromatic electromagnetic field in the resonance approximation.

For convenience, we change the notations as follows. Instead of two values i=1 and 2 of the index i labeling two states of QD, we use two symbols i=e and g to denote its excited (e) and ground (g) states with energies E_e and E_g , E_e =E_g =E> 0. We denote γ and γ⁺ as the destruction and creation operators of the photon and Ω its energy. The Jaynes–Cummings approximate expression of the total Hamiltonian is

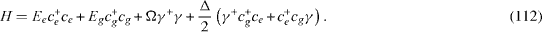
In the Hilbert space of state vectors of the quantum system with Hamiltonian (112), there is a natural basis—the Fock basis with the following orthogonal unit vectors:

From the formulae expressing the action of Hamiltonian (112) on the basis vectors (113),

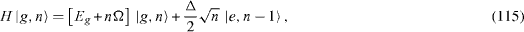
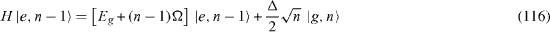
with n ≥ 1 it follows that the Hilbert space V of the state vectors of the system is a direct sum,

of a one-dimensional vector subspace V₀ with the basis vector |g,0 〉 and an infinite number of two-dimensional vector subspaces V_n , each of which is spanned on two basis vectors, |e,n- 1 〉 and |g,n〉, n ≥ 1. Basis vector |g,0 〉 is an eigenstate of H with a zero eigenvalue,

In each vector subspace, V_n , there are two orthogonal normalized eigenvectors of H,

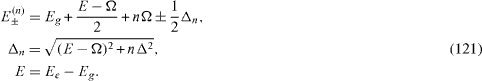
Without loss of generality, we set E_g =0 and E_e =E. Because the matrices

are unitary, the coefficients A_± ⁽ⁿ⁾andB_± ⁽ⁿ⁾for each value of n must satisfy following conditions:

Using relation (123), it is easy to invert formula (120) to express the natural basis vectors |e,n- 1 〉and |g,n〉in terms of the eigenstates of H,

The coefficients A_± ⁽ⁿ⁾and B_± ⁽ⁿ⁾for each number n ≥ 1 are determined up to a common phase factor. We choose this common phase factor in a suitable manner such that

From exact formulae (121) for the eigenvalues of the Hamiltonian (112), it is straightforward to derive an exact expression of the Lamb shift δ _L E_e as well as those of the ac Stark shifts δ _S E_e ⁽ⁿ⁾ and δ _S E_g ⁽ⁿ⁾ of the energy levels of QD in MC [32],

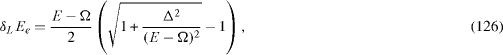
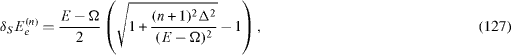
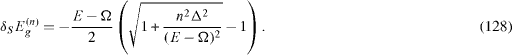
Between the ac Stark shift of the two energy level of QD, there is a simple relation,

Each pair of two states | Ψ_± ⁽ⁿ⁾〉 with a definite number n ≥ 1 can be considered as that of a free qubit. By applying the reasonings presented in section 3, we can derive exact formulae for the time evolution of the elements,

of the density matrix of the system in two-dimensional vector subspace V_n ,

From this formula and relations (124) expressing natural basis vectors in terms of eigenstate basis ones, it is straightforward to derive the exact relations determining the time evolution of the elements of the density matrix in the natural basis.

Denoting

we have

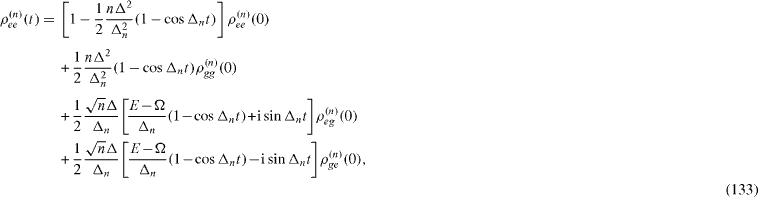
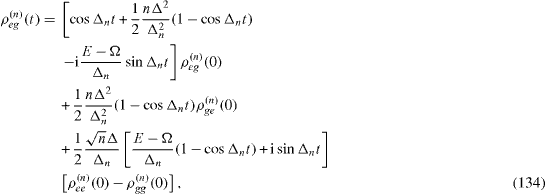
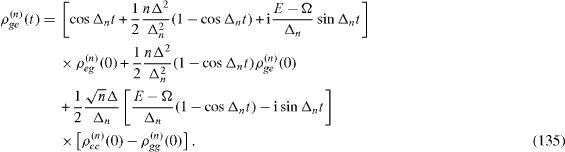
Introducing a 2×2 matrix,

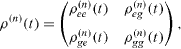
and expressing it in the form

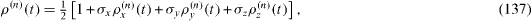
we rewrite the time evolution of the density matrix ρ ⁽ⁿ⁾ (t) in the form of the time-dependent linear transformation of a vector with three components, ρ _x ⁽ⁿ⁾ (t), ρ _y ⁽ⁿ⁾ (t) and ρ _z ⁽ⁿ⁾ (t),

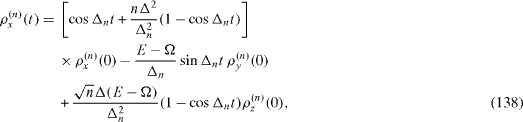
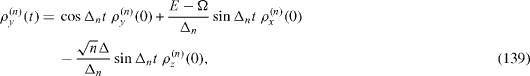
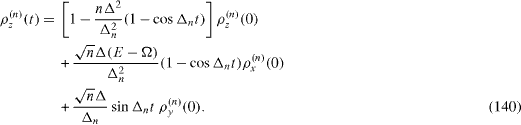
The general formula in the compact form (131) or equivalent relation (133)–(136) as well as (138)–(140) show that the quantum system with a total Hamiltonian (112) can be considered as a system consisting of a separate lowest energy state | Ψ ⁽⁰⁾〉 and a large number of independent qubits, each of which has the density matrix ρ ⁽ⁿ⁾ (t) with elements determined by formulae (132), n ≥ 1. The real existence of these qubits in the experiments depends on the initial condition: if some matrix elements (130) with a definite number n ≥ 1 have non-vanishing initial values, , then the nth qubit, whose density matrix has elements (132), does exist.

In the Jaynes–Cummings approximate expression (112) of the total Hamiltonian H, the main term of the electron–photon interaction Hamiltonian was included. However, there are other forms of the electron–photon interactions that can be treated as the perturbations. They induce the electromagnetic quantum transitions between the above presented qubits. For the theoretical study of these interaction processes, it is convenient to consider the states of the above-mentioned qubits as those of quasi-particles called CQED polarons. Thus the eigenstates of the Hamiltonian (112) considered as those of the corresponding CQED polarons can be represented in the form

where a⁽⁰⁾ ,a_σ ⁽ⁿ⁾and a⁽⁰⁾⁺ ,a_σ ⁽ⁿ⁾⁺ are the destruction and creation operators of the corresponding CQED quasi-particles and | 0 〉 is the vacuum state in the new effective formalism.

Consider a simple example: the interaction of the system with a quantum external electromagnetic field. Suppose that the Hamiltonian of this perturbation interaction has the expression

where γ _k and γ _k + are the destruction and creation operators of the external photons. Then in the new quasi-particle formalism it is replaced by the following effective interaction Hamiltonian,

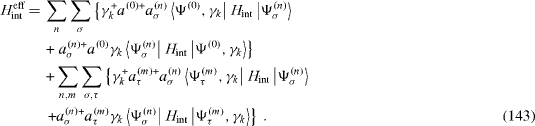
It is straightforward to derive the expressions of the effective coupling constants and .

Consider now the effect of the decoherence on the time evolution of the quantum system described by the Hamiltonian (112). There are four main physical mechanisms of the decoherence: the relaxation of electrons in the excited states of QD, the thermal excitation of electrons in the ground state of QD, the dephasing of electron transitions in QD and the leakage of photons from MC. Suppose that the system is kept at vanishing absolute temperature T=0, then the thermal excitation does not take place, and the Lindblad formula [16] for the Liouvillian superoperator can be written in the form [22, 33]

where L_r ρ is caused by the relaxation,

L_d ρ is the consequence of the dephasing,

and L_γ ρ is caused by the leakage of photons from MC,

α _r ,α_d and α _γ being three small non-negative constants, and σ₋ ,σ₊and σ ₃ being the Pauli operators acting on the natural basis vectors as follows:

In each invariant vector subspace, V_n the Liouvillian superoperator has matrix elements

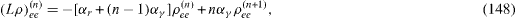
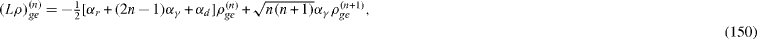
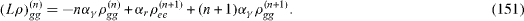
In the presence of the decoherence, each density matrix ρ ⁽ⁿ⁾ (t) is determined by the quantum Liouville (von Neumann) equation of the form [22]

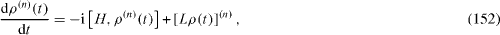
where the elements of matrix [Lρ (t) ]⁽ⁿ⁾ are given by equations (148)–(151). From the above-mentioned equations (148)–(152), we derive the system of rate equations for the elements of the density matrices ρ ⁽ⁿ⁾ (t),

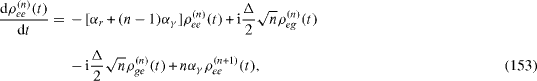
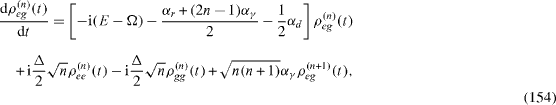
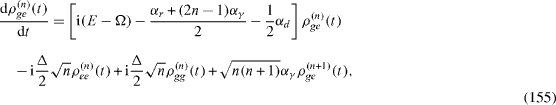
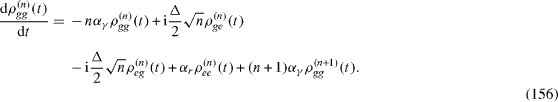
In general, each system of four equations of the forms (153)–(156) is that of four linear inhomogeneous differential equations for four functions ρ _ee ⁽ⁿ⁾ (t),ρ _eg ⁽ⁿ⁾ (t),ρ_ge ⁽ⁿ⁾ (t) and ρ _gg ⁽ⁿ⁾ (t): the rhs of these equations contains inhomogeneous terms proportional to the elements of the density matrix ρ ⁽ⁿ⁺¹⁾ (t).

The index n can be used to characterize the level of the excitation of the corresponding states |e,n- 1 〉 and|g,n〉. Their linear combinations are called nth level excited states of the electron–photon system in the single-mode MC containing a two-level QD. There always exists such a positive integer N that initial values of all elements of all density matrices ρ ⁽ⁿ⁾ (t) with n>N vanish, but the initial values of some elements of density matrix ρ ^(N) (t) are non-zero. This integer N is called the degree of excitation of the electron-photon system with total Hamiltonian (112). From the systems of equations (153)–(156) it follows that the density matrices ρ ⁽ⁿ⁾ (t) with n>N must be identically equal to zero, and four elements of the density matrix ρ ^(N) (t) satisfy the system of homogeneous linear differential equations,

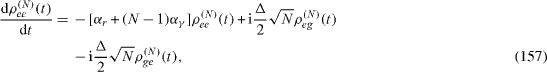
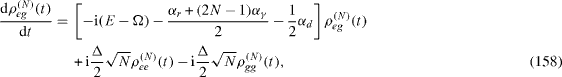
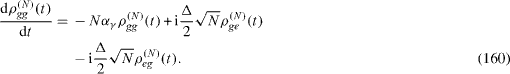
By solving the system of equations (157)–(160), we obtain explicit expressions of four elements ρ _ee ^(N) (t),ρ _eg ^(N) (t),ρ_ge ^(N) (t) and ρ _gg ^(N) (t). Using these known functions in the system of inhomogeneous linear differential equations (153)–(156) with n=N – 1 and solving the last system of equations, we derive the expressions of four elements of the density matrix ρ ^(N−1) (t). This process can be continued until all density matrices are found. The solutions of the system of equations (157)–(160) and those of equations (153)–(156) with n=N – 1 were derived in [34, 35].

At the beginning of this paper, the general formalism of the theory of reduced density matrices of two-state quantum systems to be considered as the qubits interacting with the environment was briefly presented. In particular, the quantum Liouville equation for the reduced density matrices in the Markovian approximation was introduced. To elaborate the calculation procedure, the time evolution of a free qubit was derived exactly by means of three different methods, each among which is convenient for the application to a suitable problem. One of them was then applied to the study of the coherent oscillations of a qubit interacting with a classical monochromatic electromagnetic field. The most general expressions of the Rabi oscillations were derived. The decoherence of qubits interacting with a dissipative environment was studied and the most general expressions of the reduced density matrices of the qubits were established. Finally, the quantum theory of the strongly coupled system of electrons in a two-level QD as a qubit placed inside a single-mode MC and the photons in this MC was presented. These are the basics of Cavity Quantum Electrodynamics (CQED). The quasi-particle formalism of CQED was introduced. In the study of the decoherence of this quantum system, the Lindblad formula for the Liouvillian superoperator was used. It was shown that without decoherence, the system can be considered as a set consisting of a separate lowest energy state and a large number of non-interacting qubits. However, due to the decoherence, the transitions between different qubits must take place.

The author would like to thank the Vietnam Academy of Science and Technology and Institute of Materials Science for its support.